матриц*.! ВандёрмондаР вида (4203). Новое уравнение состояния имеет вид

у(к + 1) = Лу(к) + Ги(к) (8-71) где Л= Р АР. Уравнение выхода преобразуется к виду

с(к) = Fy(k) (8-72) где F = DP. Векторы состояния х(:) и у(:) связаны соотношением

х(к) = Ру(к) (8-73)

Поскольку матрица Л является диагональной, г-е (г = 1,2,и) уравнение системы (8-71) имеет вид

У;(к-Ц)= Х;У;(к)-Ь 7;и(к) (8-74)

где - собственное значение матрицы А, - г-й элемент матрицы Г. В рассматриваемом случае Г - (иХ 1)-мерная матрица. Вьиисляя z-преобразование от обеих частей уравнения (8-74) и полагая начальные условия нулевыми, получим связь между ¥( (z) и U(z) посредством передаточной функции

U(z)

Yi() = X, Уравнение (8-72) описьшается z-преобразованием

C(z) = FY(z) = DPY(z)

Рассмотрим (IX и)-мерную матрицу

D=[d, dg ... dJ

Тогда

F=DP=[f, ... f ]

f. = dj + d2Xj+ ...+ d X

(8-75)

(8-76) (8-77) (8-78) (8-79)

для i - 1,2, n. Используя соотношения (8-75) и (8-78), запишем уравнение (8-76) в виде

C(Z) = [f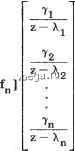

U(z)

(8-80)

C(z) Д fji U(z) 4 z - Xj

(8-81)

Последнее уравнение представляет собой передаточную функцию системы в форме элементарных слагаемых. Если в передаточной функции (8-81) имеется компенсация полюса и нуля, то соответствующий коэффициент в правой части уравнения должен быть нулевым. Предположим, что сокращается полюс Z = Ху, тогда

Отсюда следует, что либо fj- = О, либо у- = О, либо и то и другое одновременно. Поскольку есть у-й элемент матрицы Г, равенство = О оэнача-ет, что система неуправляема. в то же время, если f- = О, где fj- есть /-й элемент матрицы F, то система ненаблюдаема.

8.10. ЗАВИСИМОСТЬ УПРАВЛЯЕМОСТИ И НАБЛЮДАЕМОСТИ ОТ ПЕРИОДА КВАНТОВАНИЯ

Поскольку в цифровой системе управления присутствуют операции квантования по времени, условие управляемости и наблюдаемости может зависеть от периода квантования Т. Для импульсных систем, описьшае-мых уравнениями состояния (8-22), условие управляемости по состоянию заключается в том, что матрица Q (8-23) имеет ранг п. Это означает, что если

Qj = 0(iT)e(T) = q. = (jT)e(T) (8-82)

для г, / = 1, 2, N-l, i Ф f, к Т Ф О, то система будет неуправляемой. По аналогии из выражения (8-45) следует, что если

0(iT)d = 0(jT)d (8-83)

для i, j = 1, 2, ...,Л-1, {Ф], и ТФ О, то система будет ненаблюдаемой. Поэтому последние два условия приводят к выводу о том, что если для определенного периода квантования

ФИТ) = 0(JT)

для г, / = 1, 2, N-1, i Ф /, то система одновременно неуправляема и ненаблюдаема. в следующем примере рассматривается цифровая система, для которой зшравляемость и наблюдаемость зависят от периода квантования.

Пример 8.1. Предположим, что передаточная функция линейного процесса опи-сьшается выражением

Очевидно, что непрерывная система является управляемой и наблюдаемой, поскольку в С (s) отсутствует компенсация полюсов и нулей.

Передаточная функция G(s) заменяется следующими уравнениями состояния:

Xj(t) = X2(t) (8-85)

i2(t) = -oj\(t)-t-u(t) (8-86)

Переходная матрица состояния при замене f на Г имеет вид coscoT -wsincoT совоЯ

ф{Т) =

-sinwT

(8-87)

Поскольку COS cjT = ± 1 и sin соТ = О при соТ = тг, п=0, ± 1, ± 2,система является неуправляемой и ненаблюдаемой при cj =тг/Т.

8.11. ИЛЛЮСТРАТИВНЫЕ ПРИМЕРЫ

В этом параграфе приведено несколько примеров для иллюстрации применения рассмотренньгх выше методов проверки управляемости и наблюдаемости.

Пример 8.2. Один из методов проверки линейных систем с различными собственными значениями на управляемость состоит в диагонализации матрицы А и последующем анализе свойств строк матрицы Г, описываемой выражением (8-33). Однако некоторые матрицы А с кратными собственными значениями также могут быть диагонализированы, поэтому, хотя матрица Л является диагональной, а в матрице Г отсутствуют целиком нулевые строки, это не означает, что система является полностью управляемой. Рассмотрим цифровую систему, описываемую следующими уравнениями:

х(к -I- 1) = ах(к) 4- bjU (к) (8-88)

Х2(к -I-1) = ах2(к) -I- bgu (к) (8-89)

bi Фа, Ь2 ФО. Совершенно ясно, что зга система является неуправляемой, хотя Л - диагональная матрица, а в матрице I = [bi Ьг] отсутствуют нулевые строки. Чтобы убедиться в этом, необходимо просто составить матрицу [Г ЛГ] и показать, что она является выролщенной. С физической точки зрения состояния, описьшаемые уравнениями (8-88) и (8-89), являются несвязанными. Однако, поскольку динамика этих состояний совпадает, невозможно независимо управлять ими с помощью одной входной переменной.

Убедимся в том, что система не является управляемой по состоянию с помощью соответствующих теорем.

(Теорема 8.3) :

Q=[B АВ] =

(8-90)

Поскольку Q является вырожденной матрицей, пара [А, В] неуправляема*.

(Теорема 8.4) : Для N=2

W = АВВА4-ВВ =

(14-a2)

(8-91)

* По определению, пара [А, В] неуправляема, если система х(к+ I) -Ах(к) + + Ви (к) не является полностью управляемой- - Прим. ред. пер.