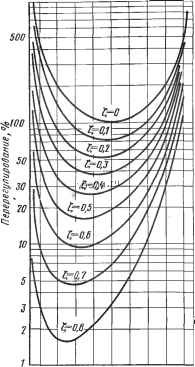Рис. 6.12. Относительное перерегулирование дискретных систем управления второго порядка

220 200 180 160

120 100 80

10 20 О

-90 -70 -50 -30 -10 О 10 30 50 tf,...

Рис. 6.13. Время максимума переходной функции дискретных систем второго порядка

-so -60-10-20 О 20 40 60а,.. При Т = ОД25 с передаточная функция замкнутой системы (6-13) принимает

83531.25(z + 1)

83644z2 + 58893,25z Н- 24525,25

(647)

Эта функция имеет нуль z = - I и два полюса z =Pi = - 0,352 /0,4114 и г = pi = = - 0,352 - /0,4114. Их положение на z-плоскости показано на рис. 6.14. Из рис. 6.14 имеем:

а = -40.66° (6 *8>

Фт=соТ= 130.55° = 2,278 рад IPl I = 0.54

Подставляя значения ipi (в радианах) и IPi I в выражение (6-45), найдем коэффициент затухания

f = 0.26

Поскохшйу а и ? известны, по номограмме (см. рис. 6.12) определяем максимальное пере1зегулирование. в данном случае интерполяция дает значение, близкое к 50 %.

,тат очшь хорошо согласуется с графиком переходной функции, показан-на рис. 6.7, на котором максимальное перерегулирование чуть больше 50 %. / Теперь рассмотрим, что будет при Т= 0,01 с. Передаточная функция замкнутой системы (6-13) имеет вид

165(z -I-1)

() 83644z2 - 160783Z + 77469

(649)

z-плоскость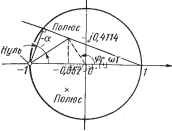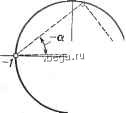

jImz

z-плоскость

o T1l

-Rez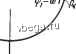

Рис. 6.14. Положение нуля и полюсов Рис. 6.15. Положение нуля и полюсов передаточной функции (6-47) при Т = передаточной функции (6-47) при Т = = 0;Z25 с = 0,01 с

Эта функция имеет нуль z = - 1 и два полюса z = р, = 0,96 + /0,0494 и z = pj = = 0,96 - /0,0494. Их положение показано на рис. 6.15, откуда имеем:

а = -37.56°

= 2.95° = 0.0514 рад ip 1 = 0.9613

Воспользовавшись соотношением (6-45), найдем коэффициент затухания замкнутой цифровой системы управления

f = 0.609

Максимальное перерегулирование, найденное с помощью рис. 6.12, составляет примерно 10 %,что очень хорошо согласуется сточным значением, определяемым по переходной функции для Т= 0,01 с, представленная на рис. 6.7.

Время максимума для двух рассмотренных выше случаев можно вьиислить непосредственно по формуле (6-46) или найти с помощью рис. 6.13. Для Т = 0,225 с. по формуле (6-46) имеем

,j 0,225

max 130,66 ДляГ= 0,01 с

arctg

-0.26

-I- 40.66° -(-180°) = 0,354 с

2,95

Т .. = [ arctg , + 37.56° 180°\ = 0.61

v/l-O.i

,609

(6-50)

(6-51)

Те же результаты можно было бы получить, воспользовавшись номограммой, приведенной на рис. 6.13. Они также очень хорошо согласуются с переходными функциями, показанными на рис. 6.7.

6.5. КОРНЕВЫЕ ГОДОГРАФЫ ЦИФРОВЫХ СИСТЕМ УПРАВЛЕНИЯ

Метод корневого годографа на s-нлоскости утвердился как полезный инструмент анализа и синтеза непрерывных систем управления. Корневой годограф непрерывной системы управления, по существу, является диаграммой траекторий корней характеристического уравнения как функ-

цией некоторого параметра К, который изменяется от - °° до °°. Корневой годограф дает возможность судить об абсолютной и относительной устойчивости системы управления в зависимости от этого параметра.

Поскольку характеристическое уравнение линейной стационарной цифровой системы управления является рациональным полиномом относительно Z, то те же правила, которые были предложены для построения корневых годографов на s-плоскости, могут быть применены и на z-плоскости. В принципе корневой годограф цифровой системы управления можно построить на s-плоскости, воспользовавшись характеристическим уравнением, полученным из полинома в знаменателе передаточной функции замкнутой системы C*(s)/R*(s), однако он будет содержать бесконечное число ветвей. Чтобы проиллюстрировать трудности анализа цифровых систем на s-плоскости, рассмотрим импульсную передаточную функцию замкнутой цифровой системы управления, заданную в виде

C*(s) G*(s) . (6-52)

R*(s) 1 -I- G*(s) где G*(s) - дискретная функция от

Итак,

G.,S) = I J G(s . in..) , К ( 4)

Известно [1], что траектории корней уравнения 1 + G*(s) = О могут быть построены на основе информации о полюсах и нулях передаточной функции разомкнутой системы G*(s). В данном случае функция G*(s) имеет бесконечное число полюсов, как показано на рис. 6.16, д. Следовательно, корневой годограф уравнения 1 + G*(s) = О содержит бесконечное число ветвей, как показано на рис. 6.16,6. Ясно, что для цифровых систем управления с более сложными передаточными функциями построение корневых годографов на s-плоскости будет более трудоемким.

Использование z-преобразования отображает бесконечное число полюсов и нулей, а значит, и траекторий корней на s-плоскости в конечное их число на z-плоскости. Для системы, описываемой уравнением (6-52), z-преобразование дает

Ш = G(z) (6-55) R(z) 1 + G(z)

а корни характеристического уравнения находят путем решения

1 + G(z) = О (6-56) где в соответствии с G(s) вида (6-53)

G(z)=/[G(s)]= Г -

(Z- l)(z- е М

Теперь траектории корней характеристического уравнения

(Z - l)(z -е-)+ К(1 - e-)z = О (6-58)