(1-Pj)(l-Pj)

(6-28)

(1-Zj)

Zl - действительный нуль; Pi uPi - комплексно-сопряженные полюсы. Мы намеренно рассматриваем здесь действительный нуль Zj, поскольку большинство непрерывных передаточных функций, не имеющих нулей, при переходе к i. -преобразованию будут давать по крайней мере один нуль. Характерным примером может служить выражение (6-11). Также намеренно мы рассматриваем только комплексные полюсы, поскольку устойчивые системы, передаточные функции которых имеют на z-плоскости действительные полюсы, не будут давать перерегулирования.

Если рассматриваемая система подвергается единичному ступенчатому воздействию, то z-преобразование выходной переменной имеет вид

zK(z-z)

C(z) =

(6-29)

(z-l)(z-pj)(z-pj)

Применяя к выраясению (6-29) формулу обращения (3-60), получим выходную переменную в моменты замыкания 1 Kz(z-z,)

где Г - замкнутый контур, включающий все особенности подьштеграль-ного выражения. Применяя к (6-30) теорему вьиетов Коши, запишем выходную последовательность с(/сТ) в виде

с(кТ) =1-1-2

(6-31)

(6-32) (6-33)

01 = arg(p-)

= arg(p ~ 1) a(Pi - 1) - й/2 На рис. 6.11 показано расположение полюсов и нуля функции (6-27).

Z -ПЛ0С/10СШ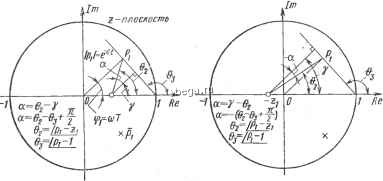

Рис. 6.11. Геометрическая интерпретация а для системы второго порядка с передаточной функцией (6-27)

Isecal = 2

(6-36)

По рисунку определим угол

±а = arg(pj - ) - arg(pj - 1) + п/2 (6-34)

где знак перед а выбирается в соответствии с ситуациями, представленными на рис. 6.11. В (6-33) мы видим, что flj связано с а соотношением

6ij = ±а - 7г (6-35)

Нетрудно показать также, что между о: и нулями и полюсами замкнутой системы имеется следующая связь:

K(Pi-z) .

(Pi - l)(Pi - Pi)

гце К определяется выражением (6-28). Подставляя (6-35) и (6-36) в (6-31), запишем выходную последовательность системы

с(кТ) = И- Isecal X р cos(k(/)± а - тг) (6-37)

Выражения (6-31) и (6-37) определяют реакцию системы с(/) только в моменты замыкания, и в принципе раз c{t) квантуется, то информация между моментами замыкания теряется. Иными словами, мы не можем восстановить.с(Г) по с(кТ). Однако можно аппроксимировать с(г) функцией, которая проходит через все точки с(кТ).

Полагая г = кТ, запишем

IPll= IPll*/ = e * (6-38)

= arg(Pi) = cjT

= c.7l-r2T (6-39)

Следовательно, непрерывная функция, которая проходит через точки с{кТ), имеет вид

c(t) = 1 + I sec а I е * cos(cjjj4/1 - f t ± а - тг) (6-40)

Максимальное значение функции c{t) используем теперь для аппроксимации выброса переходной функции цифровой системы управления, имеющей в замкнутом состоянии передаточную функцию (6-27). Максимум c(t) определяется обьшным способом, а именно приравниванием к нулю первой производной по времени выражения (6-40), что приводит к следующему соотношению:

tg(w Vl - fV ± а - тг) = - f/Vr. (6-41) Поскольку в выражении (6-41) t - время максимума

ах > то

тах =-j:-(arctg ~r==7 + a+ тг). (6-42)

Заметим, что знаки а теперь сменились на обратные.

Подставляя (6-42) в (6-40) и упрощая выражение, найдем максимальное значение

Cm ах = 1 + Vl-f I seca I exp [ J--,(arctg J- + a + тг)]. (6-43)

Следовательно, максимальное перерегулирование функции c{t), аппроксимирующей c*(t),

у/Г I secalexp [ Z- (arctg + + )]. (6-44)

Как очевидно из выражения (6-44), максимальное перерегулирование определяется исключительно коэффициентом затухания f и углом а (см. рис. 6.11).

На рис. 6.12 представлены кривые максимального перерегулирования в процентах как функции f и а. Угол а и его знак определяются по расположению нулей и полюсов передаточной функции замкнутой системы, как показано на рис. 6.11. Значение f можно вычислить, используя выражение (6-38), поскольку комплексный полюс Pi известен. На ocnonai-нии (6-38) запишем

где угол 01 выражен в радианах.

Итак, Pl известно, определяем из (6-39), после чего f вычисляем с помощью соотношения (6-45).

Время максимума Гах находим по формуле (6-42) или в виде

ОЛ / (646)

где знак а противоположен знаку этого угла на рис. 6.11.

На рис. 6.13 приведены кривые для определения Гщх. изображенные в масштабе (r iaxVi )IT как функция f и а

Следует еще раз подчеркнуть, что временная характеристика (640) является близкой аппроксимацией действительной дискретной функции c*(t) только при достаточно высокой частоте квантования. Вообще, чтобы рассмотренный здесь метод аппроксимации давал приемлемую точность, должна выполняться импульсная теорема. Или с точки зрения расположения полюсов комплексные полюса передаточной функции замкнутой системы Pl и Pl должны лежать соответственно в первом и четвертом квадрантах z-плоскости.

Как указывалось выше, рассмотренный метод может быть распространен на системы более высокого порядка, имеющие два комплексных доминирующих полюса и нуль, расположенный в любой точке на действительной оси. Остальные нули и полюсы должны находться на z-плоскости близ начала координат.

Пример 6.1. Рассмотрим цифровую систему управления космтеским кораблем (см. рис. 6.5). На рис. 6.7 изображены переходные функции этой системы для нескольких значений периода квантования Т. Определим максимальное перерегулирование и время максимума переходной функции, воспользовавшись методом, предложенным в этом параграфе. Преимущество метода заключается в том, что и перерегулирование и время максимума находят без вьиисления собственно реакции c*(f).