5.3. ЦИФГОВОЕ МОДЕЛИРОВАНИЕ. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Другой распространенный метод цифрового моделирования непрерывных систем состоит в использовании численного интегрирования. Поскольку интегрирование - наиболее трудная, требующая больишх временных затрат основная математическая операция ЭВМ, ее цифровое моделирование имеет большое значение. Вместо введения фиктивных устройств выборки и хранения в непрерывную систему в рассматриваемом методе используется приближенное описание непрерывной операции штегрирова-ния численными методами. Эта задача может быть также сформулирована как цифровое моделирование интеграторов s * на непрерьшной диаграмме состояния. На рис. 5.4 изображен интегратор как элемент диаграммы состояния. Запишем соотнощение входного и вьисодного сигналов в виде

x(t)= f*r(T)dT (5-18)

(5-19)

R(s) S

Если входной сигнал интегратора г(т) имеет вид, показанный на рис. 5.5, выходной сигнал x{t) равен площади под кривой г(т) между точками т = О и т = г.

Интегрирование по методу прямоугольников. Одним из стандартных методов численного интегрирования является метод прямоугольников, два варианта которого представлены на рис. 5.6. Интегрирование приближенно заменяется суммированием площадей прямоугольников шириной Т под ступенчатой линией, аппроксимирующей входной сигнал. Метод прямоугольников эквивалентен введению квантования совместно с экс-траполятором нулевого порядка перед каждым интегратором, как показано на рис. 5.6. Схема, представленная на рис. 5.6,а, соответствует методу прямоугольников, а на рис. 5.6,6 - методу прямоугольников с упреждением.

На основании рис. 5.6, я, можно записать дискретную передаточную функцию интегрирования по методу прямоугольников

R(z)

Ls2j

Z- 1

Уравнение состояния имеет вид

х[(к + 1)Т]= х(кТ) -I- Тг(кТ)

(5-20)

(5-21)

Рис. 5.4. Изображение интегратора в виде r(z) диаграммы состояния

rft) о-

Рис. 5.5. Связь входного и выходного сигналов интегратора

Плош,адь=хЦ)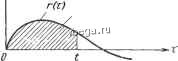

r(r)

rfz)

Аппроксимаций

r(v)

I I

0 T 2T 3T 5T

Аппроксимация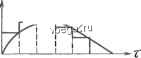

0- T 2T 3T 4T 5T

rmX.

Упрем-

дение MoT

x(t)

Рис. 5.6. Численное интегрирование по методу прямоугольников (а) и по методу прямоугольников с упреждением (б)

Аналогично запишем дискретную передаточную функцию интегрирования по методу прямоугольников с упреждением в виде

R(z)-

Ls2j

Tz z-1

(5-22)

(5-23)

a уравнение состояния в виде

х[(к -I- 1)Т] = х(кТ) -I- Тг(к -I- 1)Т

В качестве иллюстрации непрерывная система, изображенная на рис. 5.2, а, моделируется вначале с помошью интегрирования по методу прямоугольников. Диаграмма состояния цифровой модели представлена на рис. 5.7 с учетом замены интегратора 1/s передаточной функцией T/(z-l).

Преобразование вьисодного сигнала цифровой модели при единичной ступенчатой функции на входе {К=\,Т= 0,25 с) имеет вид

0.125Z

( = (z-l)(z- 0.75) (5-24)

Раскладывая C(z) в ряд, получаем

С(2;) = 0.125Z-* + 0.218z- + 0.288z-3 + 0.34z- +

+ 0.379Z-5 + 0.408z- + 0.43 Iz + QASz +

+ 0.463Z- + 0.473z- + ... . Переходная функция изображена на рис. 5.8 вместе с результатами моделирования по схеме с квантованием и фиксацией. При использовании метода прямоугольников с упреждением передаточная функция интегратора 1/s в непрерывной схеме заменяется на Tzl{z - 1).При/Г= 1 и Г =0,25 с z-преобразование выходного сигнала цифровой системы в случае единичного ступенчатого сигнала на входе имеет вид

Crz)

(Z - l)(z - 0.8)

(5-25)

а соответствующая переходная функция изображена на рис. 5.8.

Сравнение результатов показывает, что оба варианта моделирования с Использованием интегрирования по методу прямоугольников дают худ-

R(s) 1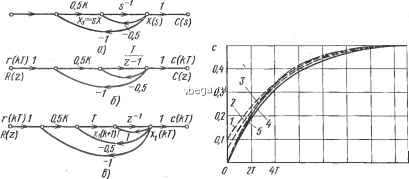

ВТ вт ЮТ пт т

Рис. 5.7. Диаграммы состояния для системы управления, язображенной на рис. 5.2, с интегрированием по методу прямоугольников:

а - диаграмма состояния непрерывной системы; б - переход к численному интегрированию по методу прямоугольников; в - диаграмма состояния цифровой модели с интегрирование по методу прямоугольников

Рис. 5.8. Сравнение различных методов цифрового моделирования: 1, 2 к 3 - соответственно интегрирование по методам прямоугольников с упреждением, трапеций и прямоугольников; 4 - схема с квантователем и экстраполятором нулевого порядка; 3 - схема с квантователем и линейным экстраполятором (непрерывная система)

шйе результаты по сравнению со схемой, использующей квантование и фиксацию. Метод прямоугольников с упреждением приводит к скачкообразному изменению выходного сигнала при г = О, хотя переходная функция оказывается близкой к истинной после значительных ошибок для нескольких первых периодов квантования.

Интегрирование по методу трапеций. Значительно более точная схема численного интегрирования получается при использовании кусочно-линейной аппроксимации, как показано на рис. 5.9, а. Площадь под кривой г(т) может быть приближенно заменена суммой площадей трапеций с основанием Т. Очевидно, что с уменьшением периода квантования Г может быть достигнута любая заданная точность аппроксимации. Этот способ приближенного интегрирования, основанный на кусочно-линейной аппроксимации, называется интегрированием по методу трапеций. Он эквивалентен введению квантователя и линейного экстраполятора перед каждым интегратором, как показано на рис. 5.9, б.

Так как передаточная функция линейного экстраполятора имеет вид

Gb(s) =

gTs + е-Т - 2 Ts2

(5-26)

то передаточная функция соответствующего метода интегрирования X(z) z+z- -2

R(z)

(5-27)