12.2. СИНТЕЗ НАБЛЮДАТЕЛЯ СОСТОЯНИЯ ПОЛНОГО ПОРЯДКА

Наблюдатель состояния, изображенный на рис. 12.1, должен проектироваться таким образом, чтобы восстанавливаемое состояние (к) было как можно ближе к действительному состоянию \(к). Существует много способов проектирования цифровых наблюдателей состояния и, как правило, несколько способов определения близости Xg(k) и х(к). Можно предположить, что наблюдатель состояния описывается такими же уравнениями состояния, как и исходная система. Однако в структуре наблюдателя, использующего и{к) и с(к) в качестве входных переменных, должна быть предусмотрена возможность автоматической минимизации отклонения х(к) от Xg (к).

Проектирование цифрового наблюдателя состояния, описываемое ниже, аналогично проектированию наблюдателя для непрерывных систем.

Поскольку х{к) не может измеряться непосредственно, нельзя сравнивать Хе(к) и х(к). Вместо этого можно сравнивать с (к) ис(к), где

с(к) = Dx(k) (12-12)

На рис. 12.2 представлена логическая структура цифрового наблюдателя состояния, основанная на предшествующих рассуждениях. Наблюдатель представляет собой замкнутую систему управленрш с матрицей обратной связи Gg. Задача проектированрш состоит в нахождении такой матрицы Gg, чтобы отклонение Cg (к) от с(к) уменьшалось как можно быстрее.

Уравнение состояния замкнутого наблюдателя имеет вид

xjk + 1) = (А - GD)x(k) + Bu(k) + Gc(k) (12-13)

где матрицы А, В и D совпадают с матрицами в уравнениях (12-2) и (12-3), а Gf - матрица обратной связи размерностью nXq. Если переменная Се(к) равна с (А:), уравнение (12-13) принимает вид

xjk + 1) = Axjk) + Bu(k) (12-14)

который идентичен уравнению состояния исходной системы.

Объединяя структурные схемы наблюдателя состояния (12-2) и цифровой системы управления (12-1), получим комбинированную систему, представленную на рис. 12.3.

Поскольку сХк) и х(к) связаны соотношением (12-3), перепишем уравнение (12-13):

хДк + 1) = Axjk) + Bu(k) + G П[х(к) - xjk)]

(12-15)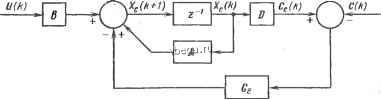

Рис. 12.2. Цифровой наблюдатель состояния с обратной связью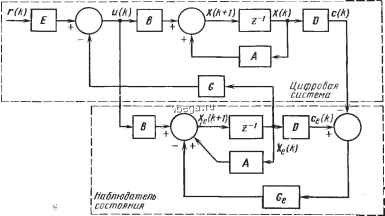

Рис. 12.3. Цифровая система управления с наблюдателем

Смысл этого уравнения состоит в том, что если совпадают начальные состояния х(0) и Хе(0), уравнение (12-15) идентично уравнению (12-14), а значит, реакция наблюдателя совпадает с реакцией исходной системы. Поэтому проектирование наблюдателя имеет смысл, когда начальные условия для х(к) HXe(fc) различны.

Вычитая уравнение (12-15) из (12-2), получим следующее выражение:

х(к + 1) - xjk + 1) = (А - G D)[x(k) - xjk)]

(12-16)

которое можно рассматривать как однородное разностное уравнение состояния линейной цифровой системы с матрицей коэффициентов А-GgD. Один из способов обеспечения быстрой сходимости Xg{k) к х{к) состоит в определении матрицы Gg из условия соответствующего размещения собственных значений А-GgD на z-плоскости. На основании методики проектирования по заданным собственным значениям, описанной в гл. 4, элементы Gg должны выбираться таким образом, чтобы траектория свободного движения системы (12-16) стремилась к нулю как можно быстрее.

Поскольку собственные значения матриц А-GD и {A-GgD) = А- -DGg совпадают, то, как следует из п. 4.13, условие произвольного размещения собственных значений А-GgD состоит в том, чтобы пара [А, D] бьша полностью управляемой. Так как управляемость [А, D] эквивалента полной наблюдаемости [А, D], выполнение этого условия будет гарантировать не только существование наблюдателя состояния, но и возможность произвольного размещения его собственных значений.

Следующий пример иллюстрирует процедуру синтеза наблюдателя состояния по заданным собственным значениям.

Пример 12.1. Рассмотрим цифровой процесс из примера 11.3 с уравнениями состояния

х(к -I- 1) = Ах(к) -I- Ви(к)

(12-17)

Пусть уравнение выхода имеет вид с(к) = Dx(k)

D=[2 0]

(12-18)

(12-19)

Необходимо спроектировать цифровой наблюдатель, который восстанавливает состояния Xi{k) и Х2 (к) по выходной переменной с ik).

Цифровой наблюдатель имеет структурную схему, изображенную на рнс. 12.2. Характеристическое уравнение наблюдателя описывается соотношением

XI-A + GgD = 0 (12-20)

x2 + (2gl-l)X+l + 2g2-2gei = 0

(12-21)

Ше gel и - элементы матрицы обратной связи Gg размч)Ностью 2X1. Спроектируем наблюдатель, имеющий апериодическую реакцию, при которой Xg (к) достигает значения х (fc) за два периода квантования. Для апериодической реакции наблюдателя необходимо, чтобы характеристическое уравнение имело вид

>2,

Х = 0

(12-22)

Таким образом, из уравнения (12-21) следует, 4Toggi =0,5 Hge2 =0. Соответствующая матрица коэффициентов для замкнутого наблюдателя имеет вид

A-GgD =

-1 -1

Для и(к) = 0 запишем уравнения состояния наблюдателя

(12-23)

xjk + 1) =

х(к)

(12-24)

Зададим произвольно начальные состояния системы и наблюдателя

х(0) =

xJO) =

0.5 О

Решим итерационно уравнения (12-17) и (12-24), начиная с заданных начальных состояний. Истинные состояния Xj {к), х (fc) и восстановленные состояния xi (к), Xg2 (KS представлены на рис. 12.4. Восстановленные состояния достигают значений действительных состояний самое большое за два периода квантования.

Замкнутая система управления с наблюдателем. В проведенном синтезе цифрового наблюдателя предполагалось, что система управления является разомкнутой, т. е. G = О (см. рис. 12.3). Для общего случая, представленного на рис. 12.3, запишем уравнения состояния следующим образом:

х(к ч- 1) = Ах(к) - BGx fk) -ь ВЕг(к)

xjk-l- 1)= (A-BG

G D)x fk) -I- G Dx(k) -b BEr(k)

(12-25) (12-26)