Сначала предположим, что обратная связь осуществляется только по переменной Xi (кТ), т. е. gi = 0. Характеристическое уравнение замкнутой системы имеет вид

Izl - А + BGI = z2 + (gj + 2)z + (1 + 3g i) = 0. (9-317)

Поскольку мы имеем только один параметр gi, то два собственных значения замкнутой системы не могут быть заданы произвольно. Разделив обе части уравнения (9-317) на члены, не содержащие gi, получим

gl(z-H3)

Т-= О (9-318)

4- 2z -И

Траектории корней уравнения (9-317), построенные на основании расположения полюсов и нулей функщш (Z -н 3)/ (z -н 2z -н 1) , изображены на рис. 9.56,с. Заметам, что при положительных значениях gj оба корня находятся вне единичной окружности, а при отрицательных один корень всегда остается слева от точки - 1 на z-плоскости. Следовательно, если обратная связь осуществляется только по переменной {кГ), то замкнутая система при любых значениях будет неустойчива.

Теперь рассмотрим случай, когда обратная связь осуществляется только по переменной Х2 (ЙГ), т. е.

G=[0 gg] (9-319)

Характеристическое уравнение замкнутой системы имеет вид

Izl - А 4- BGI = z2 -1- (gg + 2)z -f (1 - gg) = О (9-320)

Траектории корней последнего уравнения построены с помощью соотношения

1-f-r-= 0 (9-321)

z -f 2z -fl

и изображены на рис. 9.56,6. В зтом случае при отрицательных значениях g2 оба корня уравнения (9-320) находятся вне единичной окружности, а при положительных один корень всегда остается слева от точки - 1 на z-плоскости. Таким образом, при единственном входном (управляющем) воздействии с помощью неполной обратной связи по состоянию не только невозможно реализовать заданные собственные значения замкнутой системы, но и нельзя обеспечивать ее устойчивость. Изменим структуру системы, взяв матрицу В в виде

1 О О 1

В этом случае матрица обратной связи 4l Ч2

Z-плоскость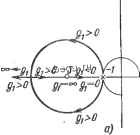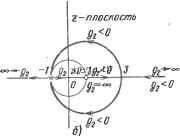

Рис. 9.56. Корневые годографы системы

Тогда

Izl - А + BGI = z2 + (2 + g + g22)z + gj(2 + g) + (1 - ggl + g) = 0

(9-322)

Если отсутствует обратная связь по Xi ikT), то = ёгг = О и уравнение (9-322) принимает вид

z + (2 + g22)z + (1 - gig) = О (9-323)

Так как в этом уравнении имеются два независимых параметра и g22, то два собственных значения матрицы A-BG можно задать произвольным образом. Аналогично при gii~g22=G имеем

z2-(2 + gll)z-г2gll + l + g2l=0 (9-324)

Опять-таки, собственные значения можно задать произвольно выбором коэффициентов gn и g2i-

Обратная связь по выходу. Поскольку выходные сигналы системы всегда доступны измерению, их можно через постоянные коэффициенты завести обратно на вход и использовать для целей управления. Таким образом, обратную связь по выходу можно считать альтернативой неполной обратной связи по состоянию.

Рассмотрим систему

х[(к -1- 1)Т] = Ах(кТ) + Ви(кТ) (9-325)

с(кТ) = Dx(kT) (9-326)

где х(кТ), и(кТ) и с(кТ) - векторы размерностью п, г ирсоответственно. Обратная связь по выходу определяется как

и(кТ) = -Gc(kT) (9-327)

где G - матрица обратной связи по выходу размерностью гХр. Целью синтеза является определение такой матрицы G, при которой будут получены желаемые собственные значения замкнутой системы. Однако, поскольку в общем случае р<г < л, не все и собственных значений могут быть заданы произвольно. Покажем, что число собственных значений, которые могут быть заданы произвольно, зависит от рангов матриц Ои В.

При синтезе системы с обратной связью по выходу можно воспользоваться тем же методом, что и в случае обратной связи по состоянию. Рассмотрим сначала случай единственного входного воздействия. Подставляя выражение (9-326) в (9-327), а затем в (9-325), получим

х[(к + 1)Т] = (А - BGD)x(kT) (9.328)

Последнее уравнение эквивалентно уравнению замкнутой системы с обратной связью по состоянию, в котором роль матрицы обратной связи играет произведение GD. Поэтому, если пара матриц [А, В] является полностью управляемой, решение для GD можно сразу получить, используя соотношение (9-244) или (9-254):

GD= [(MS)-i(a-a)] (9-329)

GD=-[Aoi - AonlK- . (9.-330)

Однако в общем случае матрицы D и DK не являются квадратными, поэтому выразить G непосредственно из двух последних уравнений не представляется возможным.

При единственном входном воздействии G имеет размерность IXр, D-рХк, аВ-иХ1, позтому GD всегда представляет собой матрицу-строку размерностью 1X п. Матрица D содержит р элементов, но только т из них соответствуют независимым параметрам, которые могут быть использованы для синтеза (здесь т - ранг матрицы G, причем m < р). Например, если

10 0

0 12 ООО

то ранг этой ТМатрицы равен 2. Если при этом G = [g ggs ], то

GD=tgi gg Sgg]

т. е. матрица GD имеет только два независимых параметра. Это означает, что с помощью обратной связи по выходу могут быть произвольно заданы лищь два из трех собственных значений системы. В случае единственного входного воздействия, если ранг матрицы D равен п, т. е. порядку системы, обратная связь по выходу дает тот же результат, что и полная обратная связь по состоянию, а именно, если пара [А, В] управляема, то все собственные значения могут быть заданы произвольным образом.

Для систем с несколькими входами В имеет размерность пХг, тогда образуется матрица

B* = Bw (9-331)

где W имеет размерность гХ 1 и содержит г параметров, а значит. В* имеет размерность иХ 1. Аналогично

G = wG* (9-332)

G*= [g* g* ... g*] (IXn) (9-333) Тогда

BGD = BwG*D = B*G*D (9-334)

и характеристическое уравнение замкнутой системы имеет вид

Izl-А+BGDI= Izl-А+B*G*D= О (9-335)

Матрицу G*D можно определить, используя соотношение (9-244) или (9-254).

В отличие от случая с единственным входным воздействием, решение для коэффициентов обратной связи по выходу теперь зависит от рангов матриц D и В. В общем случае, если ранг матрицы D больше ранга матрицы В или равен ему, элементы матрицы w могут быть выбраны произвольно, разумеется, при условии управляемости пары [А, В]. Однако при ран-