с учетом (13-5) из (13-7) следует

Q = Xo(t ). (13-7а)

В случае нестационарного объекта можно аналогично устранить время * из правых частей уравнений (13-2) формальным представлением его в виде еще одной новой координаты X объекта. Для этого к уравнениям (13-2) добавляется уравнение

Sf-- (13-8)

причем X +j (0) = 0.

В результате таких преобразований размерность фазового пространства увеличивается на два, т. е. становится равной (п + 2), а цель управления формулируется как минимизация значения одной из координат объекта в конечный момент времени.

Задача оптимального управления, в которой заданы начальные и конечные точки траектории, - это задача с фиксированными концами. Существуют так называемые задачи со свободным концом траектории, когда конечная точка траектории не задана. Они значительно проще, так как отпадает ограничение на X (fjj). Еще большее упрощение задачи получается, если задано время процесса t, т. е. в случае фиксированного времени процесса. Отметим,что обычно имеется возможность путем изменения критерия оптимальности переходить от задачи с фиксированными концевыми условиями к задаче со свободным концом или от задачи с незаданным временем к задаче с фиксированным временем процесса [30].

Определение оптимального управления U {t) и самого оптимального управляемого процесса X {t) не завершает задачи синтеза оптимальной САУ. Конечной целью синтеза является определение оператора Ауу управляющего устройства, обеспечивающего требуемое оптимальное управление и включающего в себя в самом общем случае выходную величину объекта, внешние воздействия и время:

и = Ауу(Х, X3,F,f). (13-9)

Если одно из внешних воздействий Хз или F является случайным, критерий оптимальности будет статистическим, например, в виде среднего значения функционала Q. В связи с особенностями математического аппарата в этом случае при дальнейшем изложении вопросов синтеза оптимальных САУ последние разбиты на две следующие группы: 1) оптимальные САУ, находящиеся под действием детерминированных воздействий, и 2) оптимальные САУ, находящиеся под случайными воздействиями.

§ 13-2. МЕТОДЫ НАХОЖДЕНИЯ ЭКСТРЕМУМОВ ФУНКЦИОНАЛОВ

Общим математическим аппаратом, Применяемым при синтезе оптимальных САУ, поскольку здесь речь идет о нахождении экстремумов функционалов, является вариационное исчисление,

,чая как классические вариационные методы, основанные на ениях Эйлера - Лагранжа, так и методы, созданные в пя- ятые годы нашего столетия, а именно: динамическое програм-10вание Р. Беллмана и принцип максимума Л. С. Понтрягина. Эти последние методы наиболее удобны для задач оптимального управления, поскольку наличие в этих задачах ограничений существенно усложняет применение классических вариационных методов [29]. Они предполагают применение вычислительных нашин, давая программу численного решения задачи на машине. В случае сравнительно простых задач с одним, максимум двумя управляющими воздействиями определение оптимального управления возможно методом прямого поиска путем многократного нахождения процесса на вычислительной машине при вариации равляющего воздействия [30]. В простейшем случае это может ть выполнено на вычислительных машинах непрерывного дей-щ.

Для объектов второго порядка оптимальное управление может быть найдено с помощью фазовой плоскости [29[.

, Рассмотрим метод динамического программирования и прин-максимума.

Динамическое программирование

Этот метод решения вариационных задач предложен американ-LHM ученым Р. Беллманом. В основу его положен следующий [ЦИП оптимальности: любой конечный участок оптимальной ктории является тоже оптимальной траекторией, т. е. часть [тимальной траектории от любой промежуточной точки до конца является оптимальной траекторией между этими точками, если считать ную промежуточную точку началом траектории. Сказанное иллюстрируется рис. 13-2. Принцип опти- дальности означает, что если траек-,.тория 1-2 между точками О и [яется оптимальной, то оптималь-будёт и любой ее конечный участок от произвольной точки i до точки К.

Этот принцип оптимальности не является всеобщим. Он справедлив для систем, у которых оптимальная траектория не зависит От предыстории системы, а целиком определяется исходным ее состоянием. В последнем случае справедливость принципа оптимальности очевидна: если траектория 1-2 оптимальна, обеспечивая минимум критерия, то оптимальна и траектория 2, так как, если оптимальной траекторией между точками i и К оказалась бы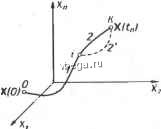

Рис. 13-2. К принципу оптимальности.

) другая траектория 2, оптимальной траекторией между О и была бы траектория 1-2, поскольку на ней крп-

какая-то

точками Сил оыла оы траектория 1-Z, поскольку на ней крп терий оптимальности имел бы меньшее значение, чем на траектории 1-2, за счет меньшего приращения его на участке 1-2.

Поясним вначале суть метода динамического программирования на следующем простом примере (рис. 13-3). Требуется перк-вести некоторый объект из точки О в точку за (т -f 1) шагов, из которых т шагов имеют I вариантов, обеспечив при этом мп- нимум критерия оптимальности Q. Этот критерий оптимальности зависит от траектории движения, и нам известна величина его приращения Д, соответствующая шагу из любой точки пути (переходу из каждой точки на рис. 13-3 в каждую точку на следующей вертикали, соответствующей концу очередного шага). Таким образом, требуется выбрать оптимальную траекторию из

Рис. 13-3. К методу динамического программирования.

точки О в точку К из конечного числа возможных траекторий, минимизирующую критерий Q. Речь может идти, например, о выборе маршрута самолета, автомобиля и т. п., проходящего через заданные точки и обеспечивающего минимум расхода горючего или времени движения. В данном случае величина Q является функцией ml переменных. Число возможных их комбинаций, т. е. число возможных вариантов решения, равно Z . При небольших вначениях т ш I оптимальное решение можно найти перебором возможных вариантов на вычислительной машине, однако в большинстве реальных задач это потребовало бы чрезвычайно большого объема вычислений. Решение этой задачи методом динамического программирования резко сокращает объем работы.

Нахождение оптимальной траектории этим методом начнем, пользуясь принципом оптимальности, с конечной точки К, пятясь к начальной точке 0. Для каждой исходной точки предпоследнего, т-го, шага найдем, например, перебором из I вариантов или любым другим методом нахождения оптимума функции (см. § 14-3, п. В) оптимальную траекторию перехода в точку К, дающую минимальное приращение йритерия оптимальности. Результаты можно представить таблицей.

решении задачи с 1[0Щью вычислительной ЯНЫ эти данные зано-в память машины.) атем, переходя к I ис-точкам предыду-{т - 1)-го, шага, кодим для каждой из оптимальную траек-в конечную точку Я составляем таблицу соответствующих значений Дмин- При этом суммарное значение Лми последних двух шагов берется из предыдущей таблицы. Аналогично находим оптимальную траекторию и значения да с начала {т - 2)-го шага и т. д., пока не дойдем до началь-точки 0. Последнее дает решение всей задачи, т. е. оптималь-траекторию в целом. Это решение, соответствующее мини-льному значению критерия оптимальности ин- определяется альной суммой из I сумм значений Д за первый шаг и иных перед этим значений А н за последующие т шагов, аким образом, в данном случае задача нахождения оптималь-- значения функции Q т переменных, каждая из которых иметь I значений, свелась к последовательному решению простой задачи нахождения оптимума функции одной [енной, имеющей I значений, т. е. с помощью динамического аммирования выбор из 1 вариантов сведен к многократному едовательному выбору всего из I вариантов. Например, для г = 10 выбор из 10° вариантов сводится к последовательному ру из 10 вариантов. Решение задачи описанным методом не обязательно требует 1ПЯТН0Г0 движения от конца к началу. Можно, например, ©нить такую процедуру расчета. Вначале для каждой из конца второго шага (рис. 13-3) находим оптимальную траек-ш (оптимальную промежуточную точку в конце первого i), дающую минимум приращения Д. Затем то же определяем каждой точки конца третьего шага, используя при этом лее найденные оптимальные решения для суммы первых двух тагов. И так действуя далее, доходим до конечной точки К. При ВТОМ в конце предпоследнего шага для каждой из Z точек оказываются найденными оптимальные траектории от начальной точки О к соответствующие значения минимального приращения Д. 1нимальная из сумм каждого из этих приращений с соответст-5щим данной точке приращением Д на последнем шаге и эделяет искомую оптимальную траекторию из точки О в конечную точку К.

Математически изложенный метод выглядит следующим образом. Предположим, что речь идет о цифровой системе с кваптова-ц нием по уровню и но времени, т. е. шаги в решении представляют

собой фиксированные интервалы времени. Требуется найти закон и (t) управления заданным объектом с учетом ряда ограничений, переводящий объект из состояния, характеризуемого точкой X (0) фазового пространства, в состояние, характеризуемое точкой X (fji), при условии обеспечения минимума критерия оптимальности в виде функционала (13-5):

Q = lG(K, Хз, и, F, t)dt.

Для дискретной системы с квантованием по времени интеграл в последнем выражении заменяется суммой функций дискретных величин, т. е.

QG\X[n],XAn],V[n],F[n],n}. (13-10)

п = 0

Здесь введено относительное время, так что п - это текущий номер периода квантования (см. § 12-2). При этом соответственно уравнение объекта записывается в конечных разностях. Задача заключается в определении управляющего воздействия U [п], т. е. последовательности его дискретных значений U [0], U [1], и [т - 1], минимизирующих сумму (13-10) при заданных уравнениях объекта и ограничениях величин U и X на его входе и выходе.

Допустим для простоты, что время процесса t фиксировано, и будем искать решение., например, опять двигаясь понятно с конечного момента t = t, т. е. в относительном времени с момента п ~ т. Решение задачи начинаем с нахождения и запоминания оптимального значения управляющего воздействия и [иг - и в начале последнего интервала для каждого возможного дискретного значения Х[т - i] (в пределах заданных ограничений последнего) и соответствующих значений приращения А , критерия оптимальности. В результате находим оптимальные значения AC>, i и U [иг - 1] как функции X [т - i].

Затем переходим к началу (т - 2)-го шага и также находим минимум приращения А 2 и соответствующее оптимальное значение U [т - 2] как функцию выходной величины системы Х[т - 2] в этот момент. Минимальное значение Д 2 для конкретного значения X [т - 2] определяем варьированием и [т - 2]. При этом для каждого значения U [иг - 2] сперва находим приращение критерия оптимальности за второй шаг и значение X [иг - 1] в конце второго шага. После этого определяем полное приращение AQ за два шага, используя ранее найденную зависимость Aj от X [иг - 1]. Переходя, далее, к началу {т - 3)-го шага и т. д., попадаем в конце концов в начальную точку X [0], определив при этом закон оптимального управления U [п], сам оптимальный процесс X [п] и суммарную величину критерия оптимальности Q. Таким образом, оптимизация функционала, зависящего от искомой функции U [и], заменяется

Едовательностью т оптимизаций значительно более простой инкции Am-i оной переменной U [т - i[. (Как уже упомина-ь, оптимум функции находится с помощью методов, изложен-в § 14-3, п. В.) Благодаря последнему упрощению метод дина-кого программирования позволяет решать задачи оптимиза- л, не решаемые классическими методами вариационного исчис-дения путем прямой оптимизации исходного функционала.

Описанную процедуру решения лишь в простейших случаях , ожно провести аналитически, т. е. с получением аналитического вырангения искомого решения. В общем же случае метод динамического программирования следует рассматривать как метод составления программы для численного решения задачи на цифровых вычислительных машинах.

Метод динамического программирования может быть применен я для оптимизации непрерывных систем путем предварительной дискретизации, т. е. приближенной замены непрерывных еменных дискретными (см. § 12-2). Правда, Беллман развил .од динамического программирования и на случай непрерывных Е[стем, однако, поскольку практически решение осуществляется цифровых вычислительных машинах, последние все равно буют проведения дискретизации.

Метод динамического программирования применяется не только t решения задач оптимизации управления. Он является общим методом решения многоходовых (много- а п н ы х) 3 а д а ч из области экономики, массового обслу-&вания, игровых ситуаций и т. д.

f. Принцип максимума

Принципу максимума л. С. Понтрягина можно дать следующую метрическую интерпретацию (рис. 13-4, а). Пусть стоит задача переводе за минимальное время изображающей точки из неко-рого начального положения О в определенное конечное К. Каждой точке фазового пространства, окружающего точку К, соответствует определенная оптимальная траектория и отвечающее ей минимальное время перехода в эту точку. Вокруг конечной чки можно построить поверхности, являющиеся геометриче-местом точек с одинаковым минимальным временем fj нере-ода в эту точку (рис. 13-4, а). Такие поверхности называются поэтому изохронами. Очевидно, что оптимальная по быстродействию траектория из точки О в конечную точку К должна быть максимально близка, нормалям к изохронам, насколько это позволяют ограничения, налагаемые на координаты объекта управления.

Действительно, всякое движение вдоль изохрон увеличивает время процесса, так как означает затрату времени без уменьшения отрезка времени, остающегося до момента достижения конечной гаки. Математически это условие оптимальности траектории