частоты, существующие на выходе импульсного элемента, не пройдут на выход непрерывной части системы, играющей роль фильтра нижних частот, импульсная система будет реагировать на низкочастотные внешние воздействия подобно непрерывной системе.

Характеристика на рис. 12-9, б соответствует выполнению первого условия (12-33), а характеристика на рис. 12-9, в не удовлетворяет ему. В результате частотная характеристика импульсной системы в пределах полосы пропускания непрерывной части системы оказывается искаженной из-за влияния боковых частот и отличается от частотной характеристики непрерывной части. Поэтому при невыполнении зтого условия импульсная САУ будет отличаться по своим свойствам от САУ непрерывного действия с той же непрерывной частью, и при ее исследовании необходимо учитывать импульсный характер работы системы (в частности, описывать ее дискретной передаточной функцией).

Второе неравенство (12-33) ограничивает частоту со приведенного внешнего воздействия таким образом, чтобы частотный спектр этого воздействия, равный после прохождения через импульсный элемент Аюп ± ю, где А; = О, 1, 2, не содержал боковых частот в пределах полосы пропускания содп непрерывной части системы, т. е. был таким же, как и при отсутствии импульсного элемента. При невьшолнении второго условия (12-33) на выходе импульсной системы будут низкочастотные состазляю-пще процесса, возникаюпще в результате прохождения внешнего воздействия через импульсный элемент и отсутствующие в непрерывной системе.

При выполнении условий (12-33) наличием квантования по времени в системе можно пренебречь и рассматривать систему как САУ непрерывного действия. Условия (12-33) представляют собой известную теорему Котельникова - Шеннона об условии неискаженной передачи непрерывного сигнала конечным числом его дискретных значений применительно к САУ с АИМ.

Частотные характеристики импульсной системы можно получить не только по дискретной передаточной функции, но и чисто графическим построением по частотной характеристике непрерывной части системы. Методика построения основана на рассмотренной выше связи дискретной передаточной функции с непрерывной передаточной функцией [16; 26].

В. Описание линейных систем автоматического управления с ШИМ

Как уже было упомянуто, импульсные элементы с ШИМ и ВИМ являются нелинейными. Однако в случае достаточно малой ширины импульсов для ШИМ или малого фазового сдвига для ВИМ (по сравнению с периодом повторения импульсов) эти оба импульсных элемента могут быть линеаризованы и сведены к эквивалентному импульсному элементу с АИМ.

Покажем это для импульсного элемента с ШИМ. Для этого

Е1вдставим импульсный элемент в виде идеального импульсного еневта с прямоугольной формой выходных импульсов. Урав-рове такого элемента имеет вид:

., У=-К\х[п]\, (12-34)

гдет = TtilTn - относительная ширина импульса; Ли - коэффици-rggr передачи импульсного элемента с ШЙМ.

Реакция приведенной непрерывной части системы на один дульс единичной высоты в соответствии с (12-29) равна

, Wn(t-m) = h{t-m) - h{t - m - yJ,

(12-35)

где Тт, согласно (12-34), равна к х1т] и является здесь в отли- чие от выражения (12-28) величиной переменной.

Соответственно после перехода к решетчатым функциям реак-на выходе непрерывной части на сигнал на входе имнульс-ого элемента

вых [ ] = а S и [п - т] sign х [т], (12-36)

где а - высота импульсов на выходе импульсного элемента.

Уравнение (12-36), которое выражает с учетом (12-35) и (12-34) а;вых[*1 через х1п], является нелинейн1м, так как Wa[n - т] представляет собой функцию х[т]. Соответственно нелинейной оказывается и система с ШИМ.

Для малых значений у выражение (12-36) можно линеаризовать, разлагая функцию w (i), являющуюся йелинейной функцией ; у, в ряд Тейлора (см. § 1-2). Действительно, при у 1 после разложения функции h{t - т - 7) в ряд Тейлора с удержанием лишь первой степени у получаем Wa{t - m)=h(i - m)--h(t-m - yjp=yji{t-m) =

= y w{t - m) = k \x[m]\w{l - m), (12-37)

?де w{f) = h(t) - весовая функция непрерывной части системы, е. ее реакция на б-импульс. При этом, согласно (12-36),

W[ ] ak-,w[n-m]x [т].

(12-38)

Уравнение (12-38) является линейным, поскольку win - m] зависит от х[т]. Применив к нему дискретное преобразование Лапласа, можно получить выражение для дискретной переда-; точной функции импульсной системы с ШИМ аналогично тому, как это делалось выше для систем с АИМ. Величина akl, в (12-38) - щ. его площадь импульса на выходе импульсного элемента при единичном входном сигнале, т. е. при х1т] = 1. Следовательно, согласно (12-38), импульсный элемент с ШИМ при V < 1 может быть еведен,как и в случае с АИМ, к идеальному импульсному элементу

с мгновенными импульсами, площадь которых пропорциональна модулирующему сигналу х. Это значит, что при 71 системы с ШИМ и АИМ эквивалентны при одинаковой зависимости площади импульсов от модулирующего сигнала х. Формально из сравнения (12-38) с выражением (12-31) для IbuxImI при АИМ следует, что при Y *С * система с ШИМ эквивалентна системе ak

С АИМ С u; [n] = u7fn].

Физически такая эквивалентность систем с АИМ и ШИМ при малой ширине импульсов -у связана с тем, что при конечной инерционности непрерывной части системы реакция ее на достаточно короткие импульсы единичной площади практические отличается от весовой функции этой части системы. Соответственно изменение Цлощади импульса вследствие изменения его высоты (при АИМ) или ширины (при ШИМ) одинаково сказывается на выходном сигнале непрерывной части системы, приводя к изменению его ординат пропорционально изменению площади входного сигнала.

Г. Особенности описания нелинейных импульсных систем автоматического управления

Импульсная САУ может быть нелинейной вследствие нелинейности импульсного элемента или непрерывной части системы. Нелинейность импульсного элемента может быть связана с нелинейностью его уравнения динамики или статической характеристики. В частности, это имеет место в случае ШИМ и ВИМ при неограниченном изменении ширины импульсов или их фазового сдвига.

Особенность математического описания не.чинейной импульсной САУ сводится к появлению в ее схеме нелинейных звеньев. Сам же аппарат описания остается прежним - это разностные уравнения с использованием для линейных частей системы дискретного преобразования Лапласа и соответственно дискретных передаточных функций.

Д. Сведение импульсной системы автоматического управления к системе непрерывного действия

Как было показано выше, в случае выполнения условий (12-33) импульсная система с АИМ может быть сведена к эквивалентной системе непрерывного действия. Передаточная функция такой эквивалентной разомкнутой САУ непрерывного действия равна АцИипСр). где Иип(р) - передаточная функция приведенной непрерывной части системы.

В случае импульсной системы с ШИМ или ВИМ условия ее эквивалентности системе непрерывного действия принимают вид:

о)пЗюн ;

(12-39)

Возможность такой эквивалентности ранее уже рассматрива-всь нами применительно к релейным САУ с вибрационной линеаризацией, где имеет место ШИМ [см. условие (11-1)]. Отличие

Бсловий (12-39) от условий (12-33) для АИМ связано с тем, что ри ШИМ и ВИМ, помимо боковых частот Люп dz Юцп, как при 1М, имеются еще и частоты dz 2юнп [25]. Правда, величина юледних составляющих довольно мала и уменьшается при умень-ении ширины (нри ШИМ) и фазового сдвига (при ВИМ) импуль-

12-3. МЕТОДЫ ИССЛЕДОВАНИЯ ИМПУЛЬСНЫХ СИСТЕМ ОМАТИЧЕСКОГО УПРАВЛЕНИЯ

При выполнении условий (12-33) или (12-39) импульсная си-сема сводится к непрерывной и, соответственно, может исследо-аться как САУ непрерывного действия методами, изложенными первой и второй частях книги. Если эти условия не выполняются, импу.чьсная САУ должна исследоваться с учетом квантования по времени, т. е. на основе описания с помощью дискретной передаточной функции или ютветствующих частотных характеристик, рассмотренных в пре-иогдущем параграфе. Это придает определенную специфику ис-Кледованию, хотя сами методы исследования точности, устойчивости и качества переходных процессов остаются прежними. W Исследование устойчивости линейных им-Ьульсных САУ осуществляется с помощью известных критериев устойчивости линейных систем - критериев Рауса - Гурвица, Щайквиста, Михайлова, модифицированных с учетом особенностей Кшсания импульсных систем.

Ш Как и у непрерывных систем, в импульсной системе переход-ная составляющая процесса управления определяется знаменателем передаточной функции WJ(z) (12-27) замкнутой системы 1 -Ь W*(z), т. е. 1 4- W*Соответственно, как и у САУ непрерывного действия, общим условием устойчивости импульсной системы является нахождение всех полюсов передаточной функции 8ам1Снутой системы, т. е. нулей 1 -f- W*(ee), в левой полуплоскости комплексной переменной q (рис. 12-10, а).

Дискретная передаточная функция Из(е) - это функция е, которая является периодической функцией мнимой части q с пе-риодом 2л, т. е.

м. § 12-3, п. Б о частотных характеристиках импульсных систем), едовательно, передаточная функция W%(e) является тоже пе-. риодической функцией вдоль мнимой оси, и поэтому при изучении полюсов этой передаточной функции в комплексной плоскости q достаточно рассмотреть их в полосе dz л вдоль действительной оси ,(рис. 12-10, я).

Если перейти от к z = еч, то нахождение нулей q многочлена 1 + W* (ев) левее мнимой оси соответствует нахождению нулей г многочлена 1 + W* (z) внутри окружности радиуса 1 с центром в начале координат (рис. 12-10, б). Иными словами, эта окружность является границей устойчивости системы в плоскости z. Действительно, при q = /со (мнимая ось) модуль z! = е == 1.

Чтобы применить критерий устойчивости Рауса - Гурвица к импул1гСной системе, произведем замену переменной, введя новую переменную w подстановкой:

(i2-40)

Области устойчивости в виде круга радиуса 1 в плоскости z (или полосы шириной ± я левее мнимой оси в плоскости д) соот-

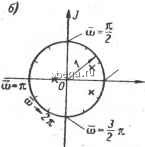Плоскость,

м=0. 2п.

Рис. 12-10. Расположение полюсов передаточной функции устойчивой импульсной системы в комплексЕшх плоскостях g и Z.

ветствует вся левая полуплоскость комплексной плоскости новой переменной w. Границей устойчивости при этом является вся мнимая ось: изменению ю на 2л соответствует изменение W от -joQ до -Ь/оо. Таким образом, в результате такой подстановки получается уравнение (передаточная функция), условия устойчивости для которого совпадают с условиями устойчивости непрерывных систем. Поэтому к нему непосредственно могут быть применены все известные для непрерывных систем критерии устойчивости. Для применения критерия Рауса - Гурвица надо использовать знаменатель D* (z) передаточной функции системы. У системы первого порядка

D* (z)=aoZ + a.

После подстановки сюда выражения (12-40) получаем

D* ( ;) = Оо J±i 4-а. = Соответствующее характеристическое уравнение будет {ao-\-aj)Kaa - a = 0,

ряовательно, условия устойчивости Рауса - Гурвица, заклю-*еся здесь в положительности коэффициентов характеристи-уравнения, сведутся к неравенству

- о> х. - (12-41)

Для системы второго порядка

Z)*(z) = aoz2-f CiZ-bfla-

Соответственно

Ш *n= .()+..(Si)+<.

{рактеристическое уравнение будет

(flo + fli + 2) w + ( о - а) И + ( о - fli + г) = О-ада получаются следующие условия устойчивости: ас + 1 + 2>0; о - 2>0;

о- 1 + 2>0.

(12-42)

аалогично можно получить условия устойчивости для сч[стем дев высоких порядков, однако они оказываются значительно лее сложными, чем в случае систем непрерывного действия. Критерий Найквиста для импульсных систем сохраняет преж-

(июю формулировку: условием устойчивости замкнутой системы, которая в разомкнутом состоянии устойчива, является неохват дмилитудно-фазовой частотной характеристикой разомкнутой системы W* (/(о) точки (-1, /0). Для иллюстрации на рис. 12-11 приведены такие характеристики импульсной системы: кривая 1 соответствует устойчивой системе, кривая 2- неустойчивой, а кривая 3 - системе, находящейся на границе устойчи-JIlDCTH. Разница по сравнению с САУ непрерывного действия Лщаключается лишь в особенностях самих амплитудно-фазовых гХарактеристик импульсных систем, которые, как показано выше, Строятся в диапазоне относительных частот 65 от О до л. Поэтому Данные характеристики не стягиваются в начало координат, а кончаются на действительной оси, как изображено на рис. 12-11.

Критерий устойчивости Михайлова для импульсных систем требует, чтобы годограф D* (eJi*), представляюпщй собой знаменатель Wt (е ), начинаясь на положительной действительной Полуоси комплексной плоскости q, охватывал начало координат, последовательно проходя 2п квадрантов, где п - порядок си-егекы. Сказанное иллюстрируется на рис. 12-12.

Исследование точности и качества нере-

1одных процессов импульсных систем осуществляется помощью тех же методов и критериев, что и в случае непрерыв-х САУ. Соответственно методы синтеза импульсных систем I .285