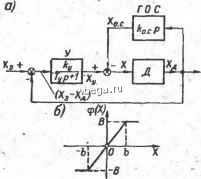Рис. 9-10. Структурная схема следящей системы.

следящей системы, структурная схема которой показана на рис. 9-10, а [18]. Система состоит из двигателя Д с постоянной времени Гд, усилителя У с постоянной Времени Ту и коэффициентом передачи ку и корректирующей гибкой обратной связи ГОС с коэффициентом передачи кол. Выходной величиной системы является угол поворота Хд вала двигателя, а вxoднoй величиной, которая отслеживается системой, - задающее воздействие Х. Двигатель представляет собой нелинейное звено вследствие ограничения скорости вращения рХ его вала. Согласно схеме, уравнение двигателя имеет вид:

{Т+1)рХ = (Х),

где ф{Х) - однозначная нечетная характеристика с насыщением, приведенная на рис. 9-10. б.

Ограничим рассмотрение случаем, когда = 0. Тогда гармоническая линеаризация нелинейности. ф(Х) дает уравнение

if{X) = k,{A)X.

Здесь, согласно приложению 6, коэффициент кг гармонической линеаризации является функцией ТОЛЬКО амплитуды А автоколебаний и равен

Ад при Л = 6;

где Ад = В/Ь - коэффициент передачи двигателя на линейном участке его характеристики ф(Х).

Соответствующий график характеристики кг(А) для такой нелинейности показан на рис. 9-9, а. В результате передаточная функция разомкнутой системы гармонически линеаризованной системы имеет вид:

где . ,

W (d) = W (п\- .

УР Typ + V *Д<>-(Гд;> + 1)р. -

Wo.c(jO) = o.cP-

Отсюда левая часть уравнения замкнутой системы, равная сумме .числителя и знаменателя W(p),

D (Р) =-{Тр +1) -Ы) jt. + [(Тр +1) Ао.е/> + А,.] А, (А) =

. / =aeP + aiJ9-baaP + 3. (9-25)

Ar =

ai=ry[l-bAo.eAr()l-f Гд; а2 = 1-ЬАо.сАг(Л); ад = АуАг(Л).

онениях от установившегося режима, соответ-0,иногда X <&, рассматриваемая система явля-В 5(том случае в (9-25) надо заменить Аг(Л) на А,.

Устойчивость в полон

При малых ствующего X ется линейно:

Условие уйойчивости такой линейной (яйстемы, согласно критерию Гурвица (см. § 4-2), имеет вид:

Д -1 = . 2- о з>0 (9-26)

при положительности всех коэф-\. фициентов и- 21 s-

На рис, 9-11 построена область устойчивости этой системы в первом квадранте плоскости коэффициентов А, и Ао.с, которые приняты в качестве варьируемых параметров системы. Область устойчивости ограничена слева осью Ао.с, на которой вз = О, а справа параболой обе, уравнение которой находится из равенства Д 1 = О и имеет вид:

1 /v-f Гд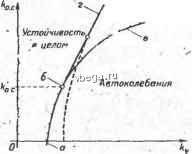

Рис. 9-11. Область устойчивости системы, изображенной па рис, 9-10.

f Лес (И-Ло-Л).

(9-27)

Определим теперь с помощью гармонической .линеаризации, как влияет не.линейность ф(Х) на устойчивость системы. Из чисто физических соображений можно предположить, что зта нелинейность характеристики двигателя должна ухудшить условия устойчивости вследствие того, что при выходе скорости двигателя из линейной зоны ±В характеристики ф(Х) ее ве-лйчина фиксируется на уровне В и поэтому перестает действовать корректирующая fгибкая обратная связь.

Возможные автоколебания в нелинейной системе определяются fiis условия наличия мнимых корней у характеристического уравнения, соответствующего дифференциальному уравнению (9-25). Если по-прежнему воспользоваться критерием Гурвица, то это условие сведется к равенству

Составленному из коэффициентов многочлена (9-25). Отсюда получаем уравнение, определяющее условия появления автоколебаний и совпадающее с уравнением (9-27), но с заменой Ад на Аг(Л):

[1-ЬЛо.Л()].

(9-28) 239

Из уравнения (9-28) можно, задаваясь значениями /су и Ло.с, найти вначале величину кт, а затем из (9-24) определить соответствующее значение амплитуды А автоколебаний. В соответствии с (9-24) автоколебания, очевидно, будут возможны при данных значениях /Суи/Со.с только в случае, если найденная величина коэффициента кг будет лежать в пределах от. /Сд до 0. В противном случае автоколебания в системе при взятых значениях ку и ко.с оказываются невозможными.

Из (9-28) видим, что при fty - оо амплитуда Л -> оо и, наоборот, чем меньше коэффициент передачи ку, тем при неизменном значении к.с будет меньше и амплитуда А возможных автоколебаний. Нас интересует граница автоколебаний в плоскости коэффициентов fty й ко.с- Она определяет для каждого значения /Со.с то минимальное, т. е. критическое, значение йу, при котором еще удовлетворяется уравнение (9-28) с учетом-(9-24) и при переходе за которое в сторону меньших ку решение (9-28) при О к кд отсутствует и, следовательно, автоколебания в системе уже нейозможнш.

Для нахождения указанного минимального значения ку надо приравнять нулю производную dky/dA, определив ее из (9-28) с учетом (9-24). Однако, поскольку

dky dky dkj.

dA dkr

и производная dk/dA на , рассматриваемом нелинейном участке зависимости ki.{A), т. е. при А Ь, везде отлична от нуля, исколгое значение ку находится из равенства нулю производной dky/dkj., оп-реде.чяемой по (9-28). В результате долучаем

h. о-с y.MHJj- у

(9-29)

При о.с < К.с минимума ку не существует во всем диапазоне кг от О до Лд. Это означает, что при любом кд.с <ко.с при уменьшении ку вплоть до значения, соответствующего границе устойчивости линейной системь!, амплитуда А уменьшается до нуля. Следовательно, при таких малых значениях ко.с граница автоколебаний совпадает с границей устойчивости линейной системы. При этом на самой границе амплитуда А автоколебаний равна нулю. На рис. 9-11 этим участком границы автоко.чебаний прио.с </Со.с является линия аб.

Граница автоколебаний при fco.cSs ко.с, соответствующая уравнению (9-29), изображена на рис. 9-11 линией бг. Каждой точке этой части границы автоколебаний соответствует своя амплитуда А автоколебаний. Она уменьшается с уменьшением ку, т. е. по мере приближения к точке б, начиная с которой и ниже Л - 0.

Область левее границы абг является областью устойчивости в целом. Она оказалась, как мы и предполагали, меньше области устойчивости, найденной при линейном рассмотрении, на область гбв. Последняя, следовательно, представляет собой область устойчивости в мязгом, но с неустойчивостью в целом.

Полученную \картину можно дополнить при необходимости построением в области автоколебаний линий постоянной амп.ли-туды Л. Онйа из них показана на рис. 9-11 пунктиром. При увеличении А эта линия будет сдвигаться вправо.

Если путем увеличения коэффициента передачи ку из области устойчивости перейти через границу автоколебаний на участке аб, в системе возникнут автоколебания, амплитуда которых будет постепенно возрастать от нуля йо мере удаления от границы. Такой характер развития автоколебаний, как указывалось в § 8-4, называется мягким возбуждением.

При переходе через границу бг уже при бесконечно малом удалении от нее возникают автоколебания конечной амплитуды, величина которой будет тем больше, чем выше система находится от точки б. Такой переход к автоколебаниям, согласно § 8-4, на- зывается .жестким возбуждением.

Соответственно с изложенным найденная при линейном рассмотрении граница устойчивости обе делится на два принципи- 1ЛЬно раз.тшчных участка. Участок аб является безопас-.ной границей устойчивости. Сколь угодно близкий подход к ней, даже небольшой переход за нее вполне допустимы. Участок бв, наоборот, является опасной границей, так как, даже не дойдя до нее, система может перейти к автоко-;лебаниям с большой амплитудой в результате воздействия достаточно большого внешнего возмущения, выводящего скорость двигателя из .т1инейного участка характеристики ф(Х).

Приведенный пример наглядно показывает, наско.лько недостаточно и опасно ограничиваться при исследовании устойчивости даже линеаризуемых в малом САУ линейным прибли-жением.

Как бы.ло ранее отмечено, после определения параметров авто-ко.лебаний в системе необходимо проверить их устойчивость, ; а также убедиться в справедливости гипотезы о том, что линейная часть системы является фильтром нижних частот. Устойчивость автоколебаний в данном случае очевидна исходя из физических соображений и результатов исследования устойчивости в .линейном приближении.

Д.ля проверки гипотезы о фильтре надо предварительно найти частоты автоколебаний. Они находятся из уравнения, получаемого приравниванием нулю. многоч.лена D{j)) (9-25) после подстановки

Выше в данном примере мы использовали критерий Гурвица. равным успехом можно было бы применить любой другой критерий устойчивости, как было показано ранее.

Мы рассмотрели методику гармонической линеаризации для случая симметричных нелинейностей при отсутствии внешних постоянных воздействий, когда автоколебания отыскиваются в виде чисто гармонических колебаний X = sintOg без постоянной составляющей.

Если характеристика нелинейного звена несимметрична относительно начала координат, автоколебания тоже будут несимметричны, т. е. будут содержать постоянную составляющую:

X = Xq -Ь Л sin (Og*.

В этом случае в результате гармонической линеаризации нелинейное звено описывается линейным уравнением (9-13):

¥У,Л-[к-р]х,

где Уо, Ар и являются функциями уже трех подлежащих определению параметров: А, (Оа т Xq.

В соответствии со схемой системы (см. рис. 9-7, а) постоянные составляющие Xq и Уо связаны передаточной функцией линейной части системы:

Хо = (0)Уо(A,w Хо). (9-30)

В скобках показано, что в результате гармонической линеаризации Уо определяется в виде функции Л, tOg и Xq.

Для гармонической составляющей система по-прежнему описывается передаточной функцией (9-20): . ..

W(pyW,ip)W(p),

W (Р) = кАА, (Dg, Хо) + И. а.а. Хо)

Методика нахождения параметров автоколебаний остается принципиально прежней с тОй только разницей, что к А и cug прибавился третий параметр Хо и соответственно новое уравнение (9-30), которое следует решать совместно с прежними уравнениями, определяющими условия существования у гармонически линеаризованной системы мнимых корней. Можно рекомендовать следующий порядок решения.

Сперва, используя передаточную функцию (9-20), описанным выше способом находим зависимости: . . -

Л {X,);

(9-31)

считая Хо варьируемым параметром. Затем, подставив эти зависимости в уравнение (9-30), определяем искомое значение А. Обычно это делается графически. После этого из (9-31) находим tOg.

Если к САУ приложено постоянное воздействие Fn, оно создает постоянный сигнал на входе нелинейного звена и автоколебания

р системе будут несимметричными даже в случае симметричной (елинейной характеристики. Уравнение для постоянной состав-чей в этом случае имеет вид:

Xo = -W (0) Уо (А, шд, Хо) -Ь Wpx (0) Fq, (9-32)

hp Wpx ~ передаточная функция между точкой приложения и X, а /0 (- иестное постоянное воздействие. ; Уравнение] (9-3S) отличается от (9-30) учетом внешнего воздей-гвяя.

В случае симметричной нелинейной характеристики уравнение 32) можнр представить в другом виде, если ввести согласно (9-19) фициент передачи постоянной составляющей автоколебаний Уд/Хо, а именно:

Изо(О)

Xo = PF3o(0)fo,. , Wfx (0) -

(9-33)

Применение гармонЬческой линеаризации для исследовання реходных процессов, вызванных медленно меняющимися здействиями, при наличии автоколебаний

Описанная выше методика исследования автоколебаний в САУ при наличии постоянного внешнего воздействия Fq может быть распространена на случай, когда внешнее воздействие не является ростоянным, но изменяется достаточно медленно по сравнению периодом автоколебаний. В частотном выражении это означает, э максимальная частота внешнего сигнала должна быть значи-яьно меньше минимальной частоты возможных автоколебаний Ьсистеме.

В этом случае внешнее воздействие, а следовательно, и но-оянную составляющую Хо на входе нелинейного звена можно ятать постоянными в течение очередного периода автоколебаний.. оэтому исходные формулы (9-12) и последующие формулы гар-онической линеаризации остаются в силе. В отличие от случая ностоянного внешнего воздействия в уравнениях (9-32) и (9-33) для постоянной составляющей теперь уже Ёельзя, разумеется, принимать р = О, и они приобретают вид:

Х{г) = -ЦАр)Уо(Л,(о,Х,)+1¥рх{р)Ро{1), (9-34)

при симметричных нелинейностях

Xo(f) = Wo{p)Fo(t), .

(9-35)

WfxW)

уво{Р)-1 (А, toa, X) Wn (рУ

Порядок нахождения решения Xf,(t) при заданном о(*) тот же, что и при постоянном о- Вначале по передаточной функции