в этом угле тем, что помимо необходимости нахождения характеристики Рл(/сй) правее точки (-Ilk, jO) требует еще возможности проведения через эту точку линии Попова. Например, в случае характеристики Wijin), изображенной на рис. 9-3, в сплошной линией, система устойчива при линейной характеристике в угле (О, к), но не обладает абсолютной устойчивостью. Точка 7 на действительной оси определяет

критический по устойчивости коэффициент передачи Ло для линейной системы, а точка 2 - критическое значение к по условию абсолютной устойчивости в случае произвольной нелинейной характеристики ф(Х). Таким образом, при произвольной форме а. ф. ч. X. ИО©) абсолютная устойчивость обеспечивается в меньшем угле, чем устойчивость в случае линейной системы.

Если характеристика Тл(7<) слева выпукла, достаточное условие устойчивости совпадает с условием устойчивости линейной системы в том же угле.

Приведенная выше формулировка критерия В. М. Попова относится к системам с устойчивой линейной частью, т. е. когда все полюсы передагочной функции левые. Чтобы

распространить этот критерий на системы с неустойчивой линейной частью, преобразуем предварительную схему системы, как это ПОК-. зано на рис. 9-4, а. Здесь в схему введены два фиктивных звена с коэффициентом передачи /Сф. Они, очевидно, ничего не изменяют в системе, так как их выходные сигналы взаимно компенсируют друг друга на входе линейной части системы. В результате получаем систему, состоящую из линейной части с передаточной функцией

и нелинейной части с хапактеюистикпй

- (9-7)

226 . - г ,

Рис. 9-4. К абсолютной устойчивости системы с неустойчивой линейной , частью.

С характеристикой -

Выберем величину коэффициента передачи кф такой, чтобы за счет введенной отрицательной жесткой обратной связи вокруг Wjiip) новая линейная часть оказалась устойчивой, т. е. все полюсы передаточной функции РГг,.ф(р) были левыми.

Заметим, что если последнее не может быть осуществлено, то ВТО уже означает отрицательный ответ на. вопрос об абсолютной устойчивости исходной системы, так как при этом она оказывается неустойчивой даже при линейной характеристике ф(Х) любого наклона.

Применим к преобразованной согласно рис. 9-4, а системе с устойчивой линейной частью критерий абсолютной устойчивости В М. Попова. В результате получим следующее условие абсолютной устойчивости исходной системы с неустойчивой линейной частью: .

ш абсолютно устойчива еслиррез точку - k - k то провести прямую линию, проходящую слева от характе-оистики л.ф(/ь))- Абсцисса указанной Т[очки определена в соответ-т с соотношением (9-7). При этом А определяется углом, в ко-ром задана характеристика fp{X).

В соответствии с критерием В. М. Попова характеристика jf{X) должна лежать в угле, ограниченном с одной стороны осью абсцисс. С учетом (9-7) это означает, что характеристика ф.(Х) должна лежать вне угла (О, кф). Таким образом, сформулированный критерий должен быть дополнен требованием, чтобы характеристика ф(Х) лежалав угле {кф, к), как показано на рис. 9-4, б. Характеристика щ{Х) при этом будет лежать в угле \0,(к - кф)].

Нетрудно видеть, что в частном случае, когда передаточная функция Wj,{p) линейной части системы имеет мнимые или нулевые полюсы при остальных левых полюсах, изложенный критерий абсолютной устойчивости совпадает с анее сформулированным критерием для случая устойчивой линейной . части, который, одйако, дополняется двумя следующими условиями. .

Во-первых, должна обеспечиватвся так называемая пре-д е ль ная устой V ивоот ь, под которой понимается устойчивость линейной системы с передаточной функцией kWjip) нри А; 0.

Во-вторых, исключается касание характеристикой нелинейного звена оси абсцисс, т. е. абсолютная устойчивость рассматривается в угле (е, к), где е - бесконечно малая величина.

Критерий В. М. Попова несложно распространить на более общий случай нелинейности, когда характеристика ц>{Х} ежит в угле {ki,), где к может быть как положительным, так и отрицательном (рис. 9-5, о). Этот случай сводится к основному случаю с характеристикой ф(Х) в угле (О, к), если представить нелинейность в следующем виде:

ф(Х) = фф(Х).+ Л,Х: (9-8).

8* . . , . 227

Здесь введвва новая нелинейность .(рф(Х), которая, согласно (9-8), получается вычитанием кх из ц>(Х). Следовательно, она лежит в угле (О, к), где к == к - к.

В результате мы получили схему, приведенную на рис. 9-5, б, где нелинейность фф(Х) лежит в угле (О, /с), а линейная часть имеет передаточную функцию

(9-9)

Выше, изучая критерий устойчивости В. М. Попова, мы имели в виду устойчивость установившегося режима системы в точке

X = 0. Однако этот критерий может быть применен и для исследования устойчивости любых динамических режимов. В этом слу-- чае, как это делалось ранее, необходимо перейти к прирап;ениям переменных X а Y относительно рассматриваемого режима и соответственно определить угол, в котором лежит нелинейность, для текущего значения переменной. В результате критерий абсолютной устойчивости процесса, вызванного ограниченным воздействием, в случае нелинейности в угле (О, Л) и устойчивой линейной части системы Сведется к следующим услорияи: 1) существование линии Попову, параллельной мнимой оси, и 2) нахождение производной характеристики ф(Х) в пределах О - Л;.

В случае неустойчивой линейной части этот критерий изменяется, как указано выше (см. рис. 9-i), введением коэффици-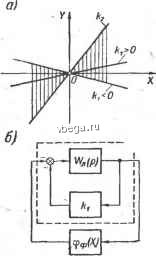

Рис. 9-5. К абссглютной устойчивости в угле {ki,kj.

ента кф [16].

§ 9-3. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ

А. Назначение метода гармонической линеаризации

Идея метода гармонической линеаризации была предложена в-1934 г. Н. М. Крыловым и Н. Н. Боголюбовым. Другие его названия - метод гармонического баланса, метод описывающих функций.

Метод гармонической линеаризации - это метод исследования автоколебаний. Он позволяет определять условия существо-

вания и параметры возможных в нелинейных системах автоколебаний.

Автоколебания определяют предельные циклы в фазовом пространстве системы, которые разделяют его на области затухающих и расходящихся процессов. Поэтому знание параметров автоколебаний позволяет представить картину всех возможных процессов в системе и, в частности, определить условия устойчивости.

Предположим, например, что в результате исследования автоколебаний в некоторой нелинейноячсистеме мы получили зависимость амплитуды этих автоколебанииу1 от коэффигщента педачи к линейной части системы, показанную на рис. 9-6, и знаем, что автоколебания устойчивы. Из графика следует, что при большом значении коэффициента передачи к, когда к fc p, в системе существуют автоколебания. Их ампли-туда уменьшается до нуля при умень-f шении коэффициента передачи к до А; р. На рис. 9-6 стрелками условно показан характер переходных процессов при разных значениях к: при к к переходный процесс, вызванный начальным отклонением, стягивается к автоколебаниям. Из рисунка видно, что при к <Акр система оказывается устойчивой. Таким образом, кр - это критическое по условию устойчивости значение коэффициента передач. Его превышение приводит к тому, что исходный режим

системы становится неустойчивым и в ней возникают автоколебания. Следовательно, знание условий существования автоколебаний в системе позволяет определить и условия устойчивости.

Метод гармонической линеаризации может быть применен и для исследования вынужденных колебательных режимов, а также для приближенной оценки качества переходных процессов в системе (см. десятую главу).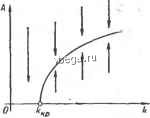

Рис. 9-6. Зависимость ами-лнтуды А автоколебаний от коэффициента передачи k системы.

Б. Идея гармонической линеаризации

Рассмотрим нелинейную систему, схема которой представлена на рис. 9-7, а. Система состоит из линейной части с передаточной функцией Wn{p) и нелинейного звена НЛ с конкретно заданной характеристикой ф(Х). По-прежнему знак - минус перед WJj)) показывает, что обратная связь в системе отрицательна. Полагаем, что в системе существуют автоколебания, амплитуду и частоту которых мы хотим найти. В рассматриваемом режиме входная величина X нелинейного звена и выходная Y являются периодическими функциями времени.

Метод гармонической линеаризации основан на предположении, что колебания на входе нелинейного звена являются синусоидальными, т. е, что

XAsinwt, (9-10)

где А - амплитуда, а (Од - частота этих автоколебаний.

В действительностр автоколебания в нелинейных системах всегда несинусоидальны вследствие искажения их формы нелинейным звеном. Поэтому указанное исходное предположение означает, что метод гармонической линеаризации является принципиально приближенный и область его применения ограничена случаями, когда автоколебания на входе нелинейного звена достаточно близки синусоидальным. Для того чтобы это имело место, линейная часть системы должна практически являться ф и л ь т -ром нижних частот и не п р о п у с к а т ь высшие гармоники автоколебаний. Последнее иллюстрируется на рис. 9-7, б, где показана возможная а. ч. х. Ап{(о) линейной части системы. Если, например, частота авто-

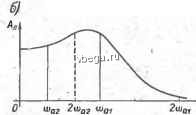Рис. 9-7. К идее гармонической линеаризации.

колебаний райна (Ogj, линейная

часть играет роль фильтра нижних частот для этих колебаний, так как уже вторая гармоника, частота которой равна 2(x)i, практически не пройдет на вход нелинейного звена. Следовательно, в этом случае метод гармонической линеаризации применим.

Если частота автоколебаний равна w, линейная часть будет свободно пропускать вторую, третью и другие гармоники авто-колебаний. В этом случае нельзя утверждать, что колебания на входе нелинейного звена будут достаточно близки синусоидальным, т. е. необходимая для применения метода гармонической линеаризации предпосылка не выполняется. Заметим, что не всегда следующей после первой гармоники будет вторая гармоника, как предположено было выше. В случае нечетных нелинейных характеристик второй гармоники на выходе нелинейного звена не будет, и условия фильтра следует проверять по третьей гармонике.

Для того чтобы установить, является ли линейная часть системы фильтром нижних частот и тем самым определить применимость метода гармонической линеаризации, необходимо знать частоту автоколебаний. Однако ее йожно узнать только в результате использования этого метода. Таким образом, применимость

гармонической линеаризации приходится определять уже конце исследования в порядке проверки. Заметим при этом, что если в результате этой проверки гипо-о том, что линейная часть системы играет роль фильтра ниж-частот, не подтверждается, это не означает еще неверности олученных результатов,-хотя, разумеется, ставит их под сом-яе и требует дополвштеьной проверки каким-либо другим

jfOflOM. ) / -

ЙИтак, предположив<Лто линейная часть системы есть фильтр аих частот, считаем, что автоколебания на входе нелинейного gBBBa синусоидальны] т. е.

еют вид (9-10).. Колебания д

иа выгоде этого звена будут при ./ТОМ уже несинусоидаль-BU вследствие их искажения нвдинейностью. В качестве Dp лера на рис. 9-8 пестрое- на кривая на выходе нели-нейного звена для определений амплитуды входного си-£&ла по характеристике la, рриведенной там же. Однако, поскольку мы ятаем, что линейная часть стемы пропускает только ювную гармонику аьтоко-вбаний, имеет смысл инте-заться только этой гар-К:оникой на выходе нели-вйного звена. Поэтому раз-выходные колебания (f) в ряд Фурье и отбросим высшие гармоники. В результате 1учим

(9-11)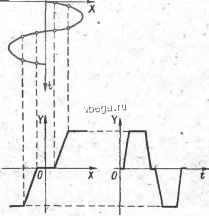

Рис. 9-8. Прохождение гармонического колебания через нелинейное звено.

№сь if

У ( ) = ф (X) =Yo-\-Ci sin (OJ + Са cos (OJ.

Yo = [f{X)dM:

-. - 2л

C = {fe{X)smwjd{wJ);

C% \ Ф Ф> COS (Oa d ((OaO;

Из (9-10)

X =i .(4 sin (Og

(9-12)