9. ту =

(ту Г 1

10. m

т + hr

2 10д.

1 + 2Ф

/fr = .-; A:j. = 0.

3 n

03. Jj

7Пу =

1 /v\

/ J

m v\

1 /m

ф8

Ox /2л

Входящие в приведенные формулы функции В (у) и С (у) определяются формулами:

\ (-l)+ [2(ft + )l!

2ft + I

ft = 0

\2ft

. n = 0,1,2...

ft = 0

При вычислении коэффициентов kp г и frp. n достаточно ограничиться! первымп четырьмя членами соответствующи.х рядов для Вп (у) и (у)-Графики этих функций приведены на рис. П-5 и П-6.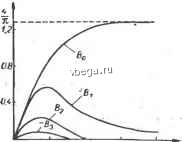

О .1 ? 3 if Рис. П-5.. График функции Ьп(у).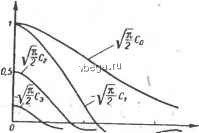

I ----Г Г

Еис. П-6. График функции Сп(у).

-Л - : :

с большой амплитудой, однако для того, чтобы они возникли, требуется соответственно очень большой внешний толчок. В результате может оказаться, что при всех практически возможных воздействиях на систему в ней могут быть только устойчивые переходные процессы. Этот случай соответствует кривым 1 ж 3 на рис. 8-9, в, если предположить, что кривая 3 расходится не до бесконечности, а до автоколебаний с определенной амплитудой. Подобный случай может быть, например, если наряду с насыщением корректирующего звена, приводящим при больших воздействиях к нарушению устойчивости с переходом от кривой 1 к кривой 3, в системе имеется еще другое последовательное звено с насыщением на значительно большем уровне, которое и ограничивает амплитуду колебаний кривой 3.

Возможны нелинейные системы, в которых в зависимости от величины внешних воздействий возникают разные автоколебания с разными амплитудами и частотами. Это иллюстрируется на рис. 8-9, д. Здесь при малых воздействиях переходные процессы стягиваются к автоколебаниям с амплитудой А, а при больших - к автоколебаниям с амплитудой (моменты времени и ifg - начала соответствующих переходных процессов).

Описанные особенности устойчивости нелинейных систем требуют при рассмотрении устойчивости таких систем оговаривать начальные условия и внешние воздействия, как это делалось ранее при рассмотрении качества линейных систем. В результате в случае нелинейных систем надо говорить не об устойчивости системы вообще, а об устойчивости определенного ее статического или динамического режима, т. е. определенного ее состояния или движения при определенных отклонениях от него. В связи с этим при изучении нелинейных систем употребляются понятия устойчивости в малом, в большом и в целом.

Устойчивость в малом - это устойчивость при бесконечно малых отклонениях от исходного режима. Устойчивость в большом - это устойчивость при конечных отклонениях, возможных в данной системе по условиям ее работы. Устойчивость в целом - это устойчивость при неограниченных отклонениях, т. е. при отсутствии каких-либо ограничений их. Нелинейная система может быть устойчива в малом, но неустойчива в большом (рис. 8-9, в). В линейных системах таких градаций устойчивости не существует, там система либо неустойчива, либо устойчива в целом. При этом в последнем случае будут устойчивы не только положения равновесия системы, но и любые вынужденные процессы.

При качественном рассмотрении процессов в нелинейных системах удобно использовать геометрическое представление, основанное на понятии о фазовом пространстве . Фазовое

Термин фаза здесь означает момент, стадию рассматриваемого процесса.

пространство - это пространство в прямоугольной системе координат Xj, которыми являются величины, определяющие состояние системы. В общем случае у системы п-то порядка таких координат будет п. Ими могут быть, например, выходная величина системы и ее (га - 1) производных, п выходных величин отдельных звеньев системы или других связанных с ними переменных, которые в совокупности полностью определяют состояние системы. Для системы второго порядка фазовое пространство двухмерное, т. е. представляет собой фазовую плоскость, а для систем третьего порядка фазовое пространство представляет собой трехмерное геометрическое пространство. При более высоком порядке п это соответственно п-мерное пространство.

Состоянию системы в каждый момент времени, определяемому значениями ее п координат, соответствует определенная точка фазового пространства. Эта точка называется изображающей точкой. На рис. 8-10, где для наглядности показано трехмерное фазовое пространство, она обозначена М. При изменении состояния системы изображающая точка будет перемещаться, описывая траекторию, которая называется фазовой траекторией. Фазовая траектория дает полное представление о характере процесса в системе, кроме его временнбй оценки, поскольку время здесь из рассмотрения исключено.

Если в качестве координат взять отклонения = Xi - XjycT величин Xi от их значений Худ, соответствующих установившемуся режиму системы, то этому режиму будет соответствовать равенство нулю всех х, т. е. начало координат фазового пространства. В этом случае для оценки устойчивости системы надо знать, как при t оо перемещается изображающая точка относительно начала координат. Для линейных систем в случае устойчивой системы все фазовые траектории асимптотически стягиваются в начало координат, а в случае неустойчивой - уходят в бесконечность.

На рис. 8-11 показаны примеры фазовых траекторий в фазовой плоскости, т. е. применительно к нелинейной системе второго порядка. Для определенности будем полагать, что Xi и х - это отклонения соответственно выходной величины и ее производной от их установившихся значений. Эти фазовые траектории описывают поведение системы после того, как она выведена из установившегося режима каким-либо воздействием, в результате чего изображающая точка оказалась в произвольном месте фазовой плоскости. Изображенные на рис. 8-11 картины фазовых траекторий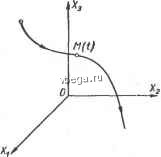

Рис. 8-10. Фазовое пространство.

называются фазовыми портретами системы Фазовые портреты, показанные на рис. 8-11, с и б, соответствуют нелинейной системе, устойчивой в малом, но неустойчивой в большом. Этим случаям отвечают переходные процессы на рис. 8-9, в.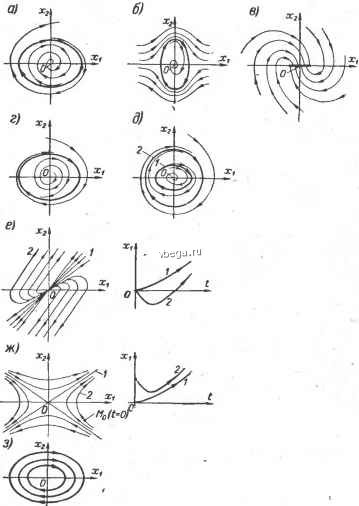

Рис. 8-11. Примеры фазовых портретов нелинейных систем.

При наличии устойчивости фазовые траектории стягиваются к началу координат, а нри неустойчивости - расходятся в бесконечность. Между этими траекториями в качестве водораздела находится замкнутая траектория, показанная толстой линией.

При колебательном переходном процессе (кривые i и 5 на рис. 8-9, в) фазовые траектории вьются вокруг начала координат вследствие периодического характера изменения координат (рис.

nil, а и область внутри замкнутой траектории на рис. 8-11, б), [еколебательному переходному процессу (кривая 2 на рис. 8-9, в) оответствуют фазовые траектории, подобные изображенным на ас. 8-11, б вне замкнутой траектории. В случае устойчивых Процессов с одним перерегулированием (рис. 8-9, а) фазовые эаектории имеют вид, изображенный на рис. 8-11, в. На этом 1 рисунке одновременно продемонстрирован случай, когда в системе имеется зона нечувствительности по переменной Х. В этом случае установившееся состояние системы определяется не началом jtOopflHHaT, а отрезком, равным зоне нечувствительности.

На рис. 8-11, г показаны фазовые траектории системы, неустойчивой в малом и имеющей устойчивый автоколебательный режим. Переходные характеристики такой системы приведены на рис. 8-9, г.

Автоколебаниям соответствует замкнутая траектория, по-1 скольку при этом переменные колеблются с постоянной амплитудой и, следовательно, изображающая точка бесконечно движется по одной и той же замкнутой траектории.

Замкнутые фазовые траектории называются предельными цик-faaMH. Они бывают устойчивыми, неустойчивыми и полуустойчи-/выми. Устойчивый предельный цикл (рис. 8-11, г) соответствует устойчивым автоколебаниям. Он характерен тем, что соседние фазоЬые траектории с обеих сторон от устойчивого предельного цикла наматываются на него. У неустойчивого предельного цикла (рис. 8-11, с) соседние фазовые траектории отходят с обеих сторон. Полуустойчивый предельный цикл соответствует промежуточному случаю, когда фазовые траектории с одной стороны приближаются к нему, а с другой отходят. Неустойчивый и полуустойчивый предельные циклы соответствуют неустойчивым автоколебаниям, которые практически в системах не существуют, являясь промежуточным состоянием при переходе от одного установившегося режима к другому.

На рис. 8-11, д показан случай с двумя предельными циклами 1 п 2. Цикл 1 неустойчивый, а цикл 2 устойчивый. Этот случай отличается от рис. 8-11, а тем, что при больших отклонениях от установившегося режима возникают колебания, которые не расходятся бесконечно, а стягиваются к установившимся автоколебаниям.

На рис. 8-11, е и ж представлены фазовые портреты неустойчивых систем с апериодической неустойчивостью. Здесь же приведены соответствующие им переходные характеристики.

На рис. 8-11,3 для сравнения изображен фазовый портрет линейной системы, находящейся на границе устойчивости вследствие того, что ее характеристическое уравнение имеет пару сопряженных мнимых корней. Здесь каждому начальному отклонению от установившегося состояния соответствует своя амплитуда незатухающих колебаний.