зацией для полученной линейной системы находим две передаточные функции - одну для детерминированной составляющей

WxiP)

W (г)- --

(8-17)

И вторую для центрированной случайной составляющей

Эти передаточные функции отличаются только коэффициентами передачи эквивалентного линейного звена. У этих коэффициентов в скобках указаны переменные, функциями которых они являются.

Из (8-17) получаем следующее выражение для т:

тх = Иео (0) тр =

(8-19)

Здесь принято р = О, поскольку тпр постоянно, и, следовательно, для детерминированной составляющей процесса имеет место установившийся статический режим (см. § 2-2).

С помощью передаточной функции (8-18) находим выражение для Ох, пользуясь формулами (3-26) и (3-34), выведенными в третьей главе для линейных систем:

Ali (o))6iro(o))do).

(8-20)

Здесь (ю) = I Hgi (jto) - амплитудная частотная функция, соответствующая передаточной функции W (р); Sp (со) - спектральная плотность внешнего воздействия {t).

Полученные уравнения (8-19) для тх и (8-20) для Ох содержат в правых частях обе искомые величины тх и в выражениях для коэффициентов kf. (тх, Ох) и к (тх, ах)- Поэтому найти значения тх и Ох можно только путем совместного решения уравнений (8-19) и (8-20). Их решают либо методом последовательных приближений, либо графически. В первом случае вначале задаются грубо приближенными значениями тх и а. Находят для них fccoH fcci. Затем по (8-19) и (8-20) определяют и в первом приближении. Они будут, естественно, отличны от ранее принятых значений. Уточнив исходные значения тх и Ох, вновь вычисляют тх и Ох во втором приближении и т. д. вплоть до момента, когда подставленные в уравнения и полученные по ним значения тх и Ох окажутся достаточно близкими.

Решение уравнений (8-19) и (8-20) графическим методом выполняют следующим образом. Вначале, задаваясь значениями тх, строят зависимость ох от тх, определяемую уравнением (8-19) (кривая 1 на рис. 8-8). Затем строят в тех же координатах зависимость <fx от тх, находя Ох по уравнению (8-20) путем подстановки в его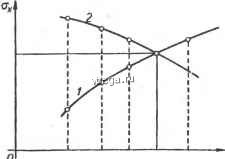

правую часть значений тх и Ох, определенных кривой / (кривая }£ на рис. 8-8). Точка пересечения обеих кривых дает искомые значения тх и Ojc, удовлетворяющие обоим уравнениям. По этим значениям определяют искомые величины коэффициентов kf. и

[ kf-i, чем и завершается первый этап исследования нелинейной САУ, т. е. линеаризация системы с определением параметров эквивалентного линейного звена.

Вторым этапом исследования является определение среднего

вначения и среднеквадратичного отклонения выходной величины

системы, находящейся в ее произвольной точке, т. е. где-то внутри линейной части (р) в схеме на рис. 8-7. Эта задача не составляет труда, поскольку мы имеем дело уже с линейной системой с извест-ными параметрами к и к. Искомые величины среднего значения

и среднеквадратичного отклоне-J ния находятся по прежним фор-It мулам (8-19) и (8-20) с тем только изменением, что в числителях соответствующих передаточных функций замкнутой системы Идо(р) и Wi (р) ставятся другие передаточные функции, связывающие F не с X, а с точкой нахождения интересующей нас выходной переменной системы.

Все изложенное выше относится к системам с одной нелинейностью в виде однозначной

нечетной характеристики. Остановимся теперь на особенностях исследования других видов нелинейных систем.

Если статическая характеристика ф (X) нелинейного звена неоднозначна, его уравнение включает помимо входной переменной X еще и ее производную X (см. позиции 3, 5, 7 приложения 5). В этом случае формулы (8-9) - (8-12) и (8-14) уже не применимы. Они должны быть усложнены учетом производной X. Выражения для kf. и к. в приложении 6 получены по этим уточненным формулам, которые, однако, мы приводить не будем, поскольку сами по себе они нам не требуются.

Если характеристика ф (X) нелинейного звена не является нечетной, т. е. несимметрична относительно начала координат (см. позиции 8-11 приложения 5), искажение левой и правой частей кривой плотности вероятности входного сигнала при прохождении его через нелинейное звено будет неодинаковым и при тх = 0. В этом легко убедиться, выполнив мысленно соответствующее построение кривой плотности р (У), аналогичное приведенному на рис. 8-4, для любой характеристики указанного

fx} /Пцз

Рис. 8-8. Графическое определение Х статистической линеа-

ризации.

вида. Поэтому в данном случае среднее значение шув нельзя выражать через тх с помощью коэффициента статистической линеаризации kf., т. е. в виде

тпгэ = кс(,тх,

так как здесь шуд Ф О при Шх = 0. В связи с этим эквивалентное линейное звено для такого вида нелинейных звеньев следует представить в виде схемы, изображенной на рис. 8-6, 6. Соответственно вместо (8-6) уравнение имеет вид:

Уэ = туэ + Уа = ту--/(;с,Х . (8-21)

Здесь к - определяемый по-прежнему коэффициент статистической линеаризации для центрированной случайной составляющей, а ту находится для однозначной нелинейности по формуле (8-9) без перехода к к. с помощью формулы (8-10).

В соответствии с изложенным для рассмотренных нелинейностей в приложении 6 вместо к даны выражения для Шу.

Согласно новому представлению эквивалентного линейного звена, оно в явном виде не замыкает систему для среднего значения, т. е. постоянной составляющей сигнала, и поэтому при исследовании точности САУ вместо уравнения (8-19) для тх следует пользоваться таким уравнением:

тх = Wpx (0) тр - (0) my {jrix, Ох). (8-22)

Здесь выражение для ту {тпх, Ох) в виде функции ти Ох берется из приложения 6.

Совместное решение этого уравнения с уравнением (8-20) для Ох дает значения т и Oje. По ним находятся значения к,. {тх. Ох) и ту {тх, Ох), т. е. определяются неизвестные параметры эквивалентной линейной САУ.

Среднеквадратичное отклонение центрированной составляющей искомой выходной величины замкнутой системы определяется далее по-прежнему. Среднее значение выходной величины в соответствии с новым представлением линейного эквивалентного звена определяется по уравнению, аналогичному (8-22), но с другими передаточными функциями, связывающими F и У на входе линейной части не с X, а с точкой нахождения выходной величины системы.

Заметим, что представление эквивалентного линейного звена в виде схемы на рис. 8-6, б с введением в рассмотрение ту вместо feco в равной мере возможно и при нечетных нелинейных характе--ристиках. Однако в этом случае получается менее наглядным взаимное влияние детерминированной и центрированной случайной составляющих сигнала, проходящего через нелинейное звено.

Описанная методика применима и к системам с несколькими нелинейными звеньями. Каждое из них заменяется эквивалентным линейным звеном, параметры которого выражаются через среднее значение и дисперсию сигнала на его входе. В результате для нахождения значений этих параметров получается система,

t состоящая уже не из двух, а из стольких пар уравнений, сколько нелинейных звеньев входит в САУ. Совместное решение этих уравнений, естественно, значительно сложнее, чем в случае одной нелинейности.

Заметим, однако, что сказанное относится к случаю, когда нелинейные звенья разделены инерционными линейными звеньями. Если же нелинейные звенья включены непосредственно друг за другом, они все сводятся к одному нелинейному звену, характеристика которого строится по характеристикам отдельных звеньев, как это описано в предыдущем параграфе.

Г. Применение статистической линеаризации для исследования нестационарных процессов с высокочастотной случайной составляющей

В заключение настоящего параграфа укажем на возможность применения статистической линеаризации для исследования нестационарных процессов, если внешнее воздействие

F{t) = mp{t) + F{t)

имеет медленно изменяющуюся во времени детерминированную составляющую тр {t) и высокочастотную стационарную случайную составляющую {t), т. е. речь идет о режиме, когда спектры детерминированной и случайной составляющих разнесены по частоте относительно друг друга.

В более общем случае случайная и детерминированная состав-I; ляющие могут представлять собой самостоятельные внешние воздействия, приложенные в разных точках системы. В частности, сюда относится практически часто встречаюнщйся случай, когда медленная детерминированная составляющая представляет собой fi задающее воздействие, а высокочастотная случайная составляющая - внешнюю помеху (шум). Задача при этом сводится к ис-г, следованию процесса отработки задающего воздействия в присутствии помех. Применив статистическую линеаризацию, по-преж->нему получим два уравнения: одно, выражающее среднеквадра-;тичное отклонение Ох центрированной случайной составляющей, \я другое - среднее значение тх детерминированной составляющей. Первое уравнение является прежним уравнением (8-20). Однако -в качестве второго уравнения уже нельзя использовать уравнение статики (8-19) [или (8-22)], полученное из (8-17) подстановкой р = О, так как теперь среднее значение сигнала непостоянно. Поэтому надо брать соответствующее ему исходное дифферен-У, циальное уравнение

к (О = p) т. (О = , т. (8-23)

Совместное решение этих двух уравнений существенно сложнее, чем в случае стационарного режима, по двум причинам.

(8-5) нелинейное звено может быть заменено тоже безынерционным эквивалентным линейным звеном, описываемым уравнением

уэ (О = туэ + у (О = К,тх -f feeix (О,

(8-6)

т. е. идеальным статическим звеном с разными коэффициентами передачи для детерминированной (коэффициент ago) случайной

(коэффициент k(.j) составляю-

щих сигнала. На рис. 8-6, а условно изображена схема этого звена, состоящая из двух параллельных звеньев. Одно (Ард) пропускает среднее значение, а другое (А) - только центрированную случайную составляющую сигнала.

Уравнение (8-6) непосредственно вытекает из условий (8-5). Согласно первому из них, коэффициент передачи эквивалентного линейного звена для среднего значения сигнала

Рнс. 8-6. Энвнвалентное линейное звено, полученное в результате статистической линеаризации.

(8-7)

в соответствии со вторым равенством (8-5) коэффициент передачи центрированной случайной составляющей сигнала

(8-8)

Действительно, возведя в квадрат уравнение

Ylit) = k Xt) - . .

и осуществив усреднение, чтобы перейти к дисперсии, получим

равенство

соответствующее выражению (8-8).

Коэффициенты к и А; называются коэффициентами статистической линеаризации или статистическими коэффициентами передачи соответственно для математического ожидания и для центрированной случайной составляющей. Коэффициенты ко и к однозначно определяются статической характеристикой у = ф {X) нёлинейного звена и законом распределения р (Х) входной величины. в соответствии с определением среднего значения [см. формулу (3-6)1

среднее значение у как неслучайной функции ф (Х) случайной величины X равно

ту = м[ф(х)]= 5 (i>{X)p{X)dX.

(8-9)

Поэтому, согласно (8-7), получаем окончательное выражение для Ко через ф (x) и j9 (x):

со = ~\ {X)piX)dX.

(8-10)

Аналогично в соответствии с определением дисперсии [см. формулу (3-10)1

Dy= 5 ipX)p{X)dX - mh (8-11)

Поэтому в соответствии с (8-8) имеем выражение

С1 -

J (p{X)p{X)dX - mY

(8-12)

Формулы (8-10) и (8-12) позволяют определить коэффициенты гатистической линеаризации к и к для заданной нелинейности ф (Х) при известном законе распределения р (Х) входной ве-(личины. в приложении 6 приведены готовые выражения для со С1 ряда типовых нелинейностей в случае нормального распределения входной величины. Функция распределения плотности вероятности для нормального закона

Как видим, для нормального закона распределения она полностью определяется значениями тпх и ах- Поэтому в случае нормального распределения коэффициенты статистической линеаризации к и afji тоже однозначно определяются через тх и ах (см. приложение 6).

При статистической линеаризации нелинейных звеньев, входящих в замкнутую систему, закон распределения случайной величины на входе этих звеньев заранее неизвестен. Поэтому его приближенно принимают нормальным и используют выражения для коэффициентов к. и к., приведенные в приложении 6. Допустимость этого связана с двумя обстоятельствами. Во-первых, при прохождении случайного сигнала через инерционную систему, какой является реальная САУ, закон распределения его приближается к нормальному и тем более, чем уже полоса пропускания линейной части системы по сравнению со спектром

7 Е. и. Юревич