Как видно из рис. 8-5, а, наличие случайной составляющей сигнала сглаживает нелинейную зависимость между выходом и входом для среднего значения, т. е. для детерминированной составляющей сигнала. При отсутствии случайной составляющей, т. е. при Gx = О, эта зависимость, естественно, совпадает с нелинейной статической характеристикой звена, а по мере роста ее наклон уменьшается, все более усредняясь, т. е. случайная

составляющая входного сигнала создает эффект линеаризации нелинейного звена для детерминированной составляющей сигнала.

Такая же линеаризация нелинейной характеристики случайной составляющей сигнала с зависимостями ту от и Ojt, подобными приведенным на рис. 8-5, а, будет, например, и в случае релейной характеристики. При этом возникает любопытное положение, когда за счет действия случайной составляющей релейное звено ведет себя по отношению к детерминированной составляющей сигнала как звено непрерывного действия.

Зависимости, показанные на рис. 8-5, б, иллюстрируют обратное влияние детерминированной составляющей сигнала на прохождение случайной составляющей. Здесь тоже с ростом тх передача звеном случайной составляющей ослабляется за счет того, что звено насыщается детерминированной составляющей сигнала.

1.0 0.8 СБ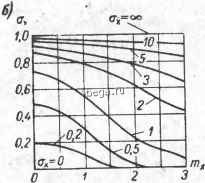

Рис. 8-5. Прохождение случайного сигнала через нелинейное звено ft насыщением.

Б. Идея статистической линеаризации .

Рассмотрим нелинейное звено (рис. 8-4, а), при подаче на вход которого стационарного случайного сигнала

\ X{t) = mx + Xt) (8-2)

установившаяся реакция на выходе тоже представляет собой Стационарный случайный сигнал

Y{t) = mY-\-Yt). - (8-3)

Каждая из составляющих последнего сигнала, как показано выше, зависит от обеих составляющих входного воздействия.

Задача статистической линеаризации заключается в том, 5ы найти линейное звено, дающее при том же входном сигнале выходной сигнал

YAt) = mYs + Ylit), (8-4)

достаточной точностью приближающийся к сигналу Y (t). Точность линеаризации зависит от того, какой выбран крите-ш для сравнения Y с Y. Наиболее распространенными крите-шми статистической линеаризации являются следующие два. рервый состоит в том, что уравнение эквивалентного линейного ввена определяется по условию сохранения неизменными среднего значения и дисперсии выходного сигнала, т. е. исходя из следующих равенств:

(8-5)

Второй критерий заключается в определении уравнения экви-

Fлентного линейного звена по условию минимума среднеквадра чного отклонения Уд (t) от Y {t). Рассмотрим вначале статистическую линеаризацию на основе аервого критерия, т. е. по условию (8-5). При выполнении первого условия (8-5) линейное звено будет полностью эквивалентно Ьсходному нелинейному в отношении пропускания заданной детер-инированной составляющей входного сигнала. Второе условие В-5) является условием эквивалентности в отношении пропуска-Кия центрированной случайной составляющей входного сигнала. В связи с тем, что дисперсия не определяет полностью закона распределения случайной величины, выбор уравнения эквивалентного линейного звена исходя только из дисперсии случайной Ьоставляющей входного воздействия определяет погрешность ранной статистической линеаризации.

Например, при статистической линеаризации нелинейного вена с насыщением (см. рис. 8-4) на выходе эквивалентного ейного звена вместо случайной величины с законом распреде-ия, изображенным на рис. 8-4, г, будет случайная величина тем же законом распределения, что и входная величина (см. НС. 8-4, в), но со средним значением и дисперсией, совпадающими значениями для истинной кривой на рис. 8-4, г. Т. е. прибли-ость статистической линеаризации заключается в пренебре-ении искажением закона распределения случайного сигнала, осуществляемым нелинейным звеном. Эта приближенность, в свою очередь, приводит к тому, что оценка точности замкнутых САУ, выполняемая с помощью этого метода, является принципиально приближенной.

Для упрощения дальнейшего изложения ограничим пока свое рассмотрение безынерционными нелинейными звеньями, описываемыми однозначной нечетной статической характеристикой (Позиции 1, 2,3,6 приложения,5). В этом случае исходя из условия

СО-первых, входящие в эти уравнения коэффициенты к и А-, теперь не постоянны, а медленно изменнются во времени вместе с Шр (О- Во-вторых, второе уравнение для детерминированной составляющей из алгебраического стало дифференциальным (8-23).

Однако благодаря тому, что детерминированная Составляющая является медленной по сравнению со случайной, задача существенно облегчается возможностью при решении уравнения (8-20) для случайной составляющей сигнала считать процесс квазистационарным и применить известный нам по § 7-3, п. Б метод замораживания коэффициента к., т. е. решать это уравнение по-старому, полагая этот коэффициент постоянным.

Графическое решение уравнения (8-20) дает определяемую им зависимость ох от тх- Подставив эту зависимость в выражение для (тх, Ох), получим нелинейную зависимость кс{тх) только от тх. Подставив ее в уравнение (8-23) для детерминированной составляющей, получим нелинейное уравнение, содержащее только детерминированную составляющую:

(8-24)

Решение этого уравнения дает искомый процесс (t). В дальнейшем по найденным значениям тхж ох можно описанным ранее способом найти детерминированную и случайную составляющие процесса в любой точке системы.

Решение нелинейного дифференциального уравнения (8-24) облегчается тем, что входящая в него нелинейная зависимость fco от /пх обычно, во всяком случае при достаточно большой случайной составляющей, очень слаба, т. е. в широком диапазоне изменения тх можно считать к постоянным. При этом уравнение (8-24) становится линеаризуемым и его решение не представляет труда.

Слабая зависимость к от тх объясняется описанным выше явлением сглаживания нелинейностей случайным сигналом. Например, как следует из рис. 8-5, а, в случае нелинейности типа насыщения с ростом Ох, т. е. случайной составляющей сигнала, зависимость ту от тх все более сглаживается и соответственно статистический коэффициент передачи к = ту/тх, уменьшаясь, все более стабилизируется относительно тх-

Описанное влияние высокочастотной случайной составляющей на коэффициент передачи нелинейного звена для детерминированной составляющей создает характерные особенности динамики нелинейных систем, отсутствующие в линейных системах. В частности, если высокочастотная случайная составляющая представляет собой помеху, то при изменении уровня помехи будут изменяться точность и качество реакции САУ на детерминированные воздействия. Например, если, как в рассмотренном выше случае, с ростом уровня случайной помехи величина коэффициента

уменьшается, это эначит, что одновременно падают точность и быстродействие детерминированных процессов управления.

Более того, за счет изменения уровня случайной помехи нелинейная САУ может из устойчивой превратиться в неустойчи-. вую и наоборот. Например, нелршейная САУ с линеаризуемой I нелинейностью в виде насыщения, неустойчивая вследствие того. что ее коэффициент передачи выше критического по условию устойчивости, может быть сделана устойчивой путем приложения к ней случайного сигнала. Обратное превращение устойчивой САУ в неустойчивую случайной помехой возможно, в частности, если ту же характеристику с насыщением имеет корректирующее звено, которое стабилизирует систему.

Рассмотренное влияние случайной помехи на устойчивость нелинейной САУ представляет собой совершенно новое явление, не укладывающееся во введенное ранее применительно к линейным системам понятие об устойчивости. Там мы привыкли, что устойчивость есть внутреннее свойство системы, не зависящее от внешних воздействий. Б случае же нелинейных систем, оказывается, устойчивая система, имеющая затухающую переходную характеристику, может начать раскачиваться при приложении к ней ограниченной по величине случайной помехи или при воз-викновении ее внутри самой системы.

У Б ходе рассмотрения статистической линеаризации мы перешли t к вопросу об особенностях динамики нелинейных систем, являю-рщемуся предметом следующего параграфа. Однако, прежде чем окончательно остановиться на рассмотрении этого вопроса, в заключение отметим еще одно важное обстоятельство в отношении применимости статистической линеаризации. Использование статистической линеаризации предполагает, что исследуемая система устойчива и в ней отсутствуют незатухаюхцие колебания. В противном случае вследствие неприменимости к нелинейным системам принципа суперпозиции необходимо при статистической линеаризации учесть прохождение через нелинейное звено этих колебаний. Для этого применяется метод совместной статистической и гармонической линеаризации, о котором будет сказано позднее в § 9-3.

Более подробно о статистической линеаризации см. в работах [6; 14].

§ 8-4. ОСОБЕННОСТИ ДИНАМИКИ НЕЛИНЕЙНЫХ СИСТЕМ

Быше при рассмотрении установившихся режимов нелинейных САУ было выяснено, что в отличие от линейных систем точность нелинейных систем зависит от величины внешних воздействий. Такая же зависимость существует и в отношении устойчивости и качества переходных процессов в нелинейных системах.

У линейных систем, как было показано в первой части книги, точность, устойчивость и качество переходных процессов не зависят от величины внешних воздействий. Благодаря применимости

внешнего воздействия. Поэтому даже тогда, когда приложенное к САУ внешнее воздействие имеет распределение, далекое от нормального, распределение случайной величины, попадающей на входящее в систему нелинейное звено, будет значительно ближе к нормальному. Во-вторых, расчеты показывают, что при изменении в широких пределах закона распределения величины на входе нелинейного звена значения kf. и к изменяются незначительно.

Таким образом, в целом приближенность расчетов методом статистической линеаризации связана с допущением, что величина на входе нелинейного звена ижет нормальное распределение, и, далее, с неучетом искажения этого закона нелинейным звеном. При этом действительный закон распределения величины на выходе нелинейного звена заменяется тоже нормальным с сохранением прежних среднего значения и дисперсии. Погрешность расчетов, основанных на статистической линеаризации, будет тем меньше, чем ближе распределение внешнего воздействия к нормальному и чем шире его частотный спектр Но сравнению с полосой пропускания линейной части системы.

Выше была изложена идея статистической линеаризации, основанная на условиях (8-5), т. е. равенстве средних значений и дисперсий величин У и Уд.

Остановимся теперь на другой возможной статистической линеаризации, основанной на критерии минимизации среднеквадратичного отклонения Уд от У. В этом случае уравнение эквивалентного линейного звена определяется исходя из условия

М[(У-Уэ)21 = тш.

Можно показать, что и здесь статистическая линеаризация безынерционного нелинейного звена тоже сводится к замене нелинейного звена идеальным линейным с разными коэффициентами передачи для среднего значения и центрированной случайной составляющей. При этом значение первого коэффициента статистической линеаризации совпадает е ранее найденным по первому условию (8-5) коэффициентом к.. Выражение для второго коэффициента статистической линеаризации получается другим:

Отсюда

(8-13)

(8-14)

В приложении 6 приведены также выражения и для этого коэффициента к- Как видно, этот способ линеаризации дает более простые выражения для к. и поэтому более предпочтителен.

Погрешность расчетов точности САУ, основанных на последней и ранее изложенной идеях статистической линеаризации, как

; показывает опыт, в обоих случаях получается примерно одинаковой ,по величине, хотя, как правило, разных знаков. В связи с этим рекомендуется для повышения точности расчетов использовагь в качестве коэффициента А:. среднее арифметическое значение этого коэффициента, полученное обоими способами, т. е. брать

Ь<1 Ь2>

С1 1

(8-15)

где kii и кЦ - значения /с, соответствующие первому и второму юсобам статистической линеаризации.

Методика исследования точности нелинейных САУ с йомощью статистической линеаризации

Рассмотрим замкнутую САУ, изображенную на рис. 8-7. В хроизвольной точке системы приложено стационарное случайное воздействие

F(t) = nlp-\-F it), . (8-16)

создающее в системе стационарный случайный режим. Минус на вхо-линейного звена (р) показывает, что обратная связь в системе отрицательна. Наша задача заключается в том, чтобы определить реднее значение и дисперсию выходной величины САУ, которая в общем случае тоже нахо-

Ylthmy--Y>(t)

Рис. 8-7. Статистическая линеаризация нелинейной замкнутой системы.

едится в произвольной точке системы.

Первым этапом решения 1вляется осуществление ста-1Стической линеаризации 1елинейного звена. Полагая, 1Т0 X it) имеет нормальное распределение, осуществляем статистическую линеариза-р,цию нелинейного звена, заме- нив его идеальным статиче-

ским звеном, показанным на рис. 8-6, а, с коэффициентом передачи для среднего значения л коэффициентом передачи fej для центри-[[рованной случайной составляющей входной величины X {t). ЕЭти коэффициенты находятся по приложению 6 в виде функций 1ока неизвестных величин тх и Ojf, которые, таким образом, нам )бходимо найти, чтобы определить значения к,. и к.. Заметим, что полученная в результате линеаризации САУ является линейной только при фиксированных тх и О;, т. е. при Стационарном воздействии на систему, но при изменении этого Воздействия она по-прежнему нелинейна, так как содержит коэф-щиентм, зависящие от тх Ох-Для нахождения тх и Ох можем применить известные нам мето-теории линейных САУ. В соответствии с проведенной линеари-