от критического положения, при котором система находится па границе устойчивости. Для критерия Михайлова это будет удаление годографа D (/со) от начала координат, а для критерия Найквиста - удаление характеристики (/со) от точки ( - 1, /0).

Основное расиространение в качестве меры запаса устойчивости получшги вытекающие из критерия На11квиста две величины - запас устойчивости по фазе Дер и запас устойчивости по амплитуде IS.L. Эти величины показаны на рнс. 4-5 для системы с л. ф. х., представленной кривой 1. Аналогично они люгут быть найдены и по а. ф. ч. X.

Запас устойчивости по фазе определяется ве-личино!! Дф, на которую долншо возрасти запаздывание по фазе в системе на частоте среза со чтобы система оказа.лась на границе

УСТ011ЧИВ0СТИ.

Запас у с т о й ч п в о с т п по амплитуде определяется величиной ДЬ допустимого подъема л. а.х., при котором спстема окажется на границе устойчивости. Таким образом, запас по амплитуде представляет собой запас по коэффициенту пересдачи к разомкнутой спстемы по отношению к его критическому по устойчивости значению.

При проектировании САУ рекомендуется выбирать Дф ,30°, а IS.L 6 дб. Последнее соответствует примерно двойному запасу коэффициента передачи по устойчивости.

§ 4-5. ОБЛАСТИ УСТОПЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЙ

При синтезе САУ, когда требуется определить влияние значений каких-либо варьируемыхпараметров на устойчивость, строят область устойчивости системы в пространстве этих варьируемых параметров.

Область устойчивости определяет совокупность значений параметров системы, при которых cиcтeш устойчива.

В случае, если варьируемых параметров два, область устойчивости изображается на плоскости, как показано на рис. 4-6. а. Здесь А и В варьируемые параметры. На рисунке линией изображена граница устойчивости. Для указания, с какой стороны границы находится область устопчивости, вдоль границы наносится штриховка, которая обращена в сторону об,т1асти устойчивости. В данном случае область устойчивости является замкнутой, что, однако, необязательно. Каждая точка внутри области устойчивости (рис. 4-6, а) определяет комбинацию варьируемых параметров А и fi-, при которых система устойчива.

Все пространство вне области устойчивости называется областью и е у с т о й ч и во с т и. Все точки ее соответствуют значениям параметров, при которых система неустойчива.

При трех варьируемых параметрах область устойчивости получается трехмерной, как показано на рис. 4-6, б, где А, В п С - варьируемйе параметры. Граница устопчивости при этом представляет собой трехмерную поверхность. При практических расчетах в этом случае область устойчивости изображается, как показано на рис. 4-6, в, тоже в плоскости двух параметров в виде граттц устойчивости, соответствующих нескольким фиксирован-

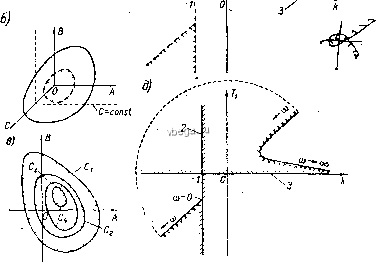Рпс. 4-6. Области устоичзшости САУ.

ным значениям третьего параметра. Это соответствует сечениям исходнойобласти устойчивости рядом плоскостей, определяемых фиксированньпш значения.лш одного параметра (см. пунктпр на рис. 4-6, б).

В общем случае д варьируемых параметров область устойчивости представляет собой гиперповерхность в тг-мерном пространстве.

Если система в пространстве всех своих параметров не имеет области устойчивости, она называется структурно не-У с т о й ч и в о й. Структурно неустойчивая система не может быть сделана устойчивой путем изменения значений всех ее параметров. Для получения устойчивости в эхом случае необходимо изменить структурную схему системы.

Построение границы устойчивости осуществляется с помощью критериев устойчивости. В качестве примера на рис. 4-6, г с помощью критерия Гурвица построена граница области устойчивости для системы третьего порядка с передаточной функцией (4-8), рассмотренно!! выше при изложении этого критерия устойчивости. Граница устойчивости построена в плоскости коэффициента передачи /с разомкнутой системы и одной из постоянных времени Т. Область устойчивости получилась незамкнутой. Она ограничена тремя линиями 1, 2 \\ 3. Уравнения этих границ области .устойчивости получаются из условий устойчивости Гурвица (4-8а) для этой системы, если заменить в них неравенства равенствами, что соответствует нахождению системы на границе устойчивости. Граница 1 j;ooTBeTCTByeT последнему условию (4-8а), которое дает уравнение границы в виде (4-8в). По этому уравнению можно построить границу i, задаваясь, например, значениями варьируемого параметра Ту и находя соответствующие критические по устойчивости значения к, при которых система оказывается на границе устойчивости.

Граница 2 соответствует предпоследнему условию (4-8а), которое дает уравнение этой границы в виде:

к~\.

Граница 3 определяется первым условием (4-8а), которое дает лфавнение

Выше мы полагали, что постоянная времени - величина положительная. Интересно отметить, что если ввести в рассмотрение отрицательные значения Т, то, согласно условиям устойчивости (4-8а), в плоскости параметров к, Т появится новая часть области устойчивости в третьем квадранте, которая показана на рис. 4-6, г пунктиром.

В общем случае границы области устойчивости по критерию Рауса - Гурвица строятся по следующим уравнениям:

Дп-1 = 0;

= 0; -0.

(4-10)

Как известно из алгебры, здесь первое уравнение, т. е. равенство нулю предпоследнего минора Гурвица, соответствует на.личию у характеристического уравнения (4-6)

пары сопряженных мнимых корней; второе равенство соответствует наличию нулевого корня, а третье - наличию бесконечного корня.

Эти три уравнения охватывают три возможных случая,попадания системы на границу устойчивости, т. е., иными словами.

три принципиально возможных пути перехода какого-лиоо корня характеристического уравнения с левой комплексной полуплоскости направую. Первый путь соответствует превращению какой-либо пары комплексных корней в чисто мнимые, т. е. переходу этих корней из левой полуплоскости на мнимую ось и, соответственно, возникновению в системе незатухающих колебаний. Второй путь соответствует превращению одного из действительных корней в нулевой, т. е. переходу его в начало координат, а третий - превращению этого корня в бесконечный корень, т. е. переходу его из левой полуплоскости в бесконечность. Последние два с.чу-чая учитывают возможность перехода корня из .левой полуплоскости в правую, минуя превращение его в мнимый корень, через начало координат или бесконечность.

Варьируемые параметры А п В, в плоскости которых строится область устойчивости, входят в выражения для Д 1 (А,В), а,{А,В) и ао {А,В) в .(4-10).

После построения линий, соответствующих уравнениям (4-10), плоскость варьируемых параметров оказывается разделенной на ряд областей, из числа которых надо найти область устойчивости. Обычно она бывает очевидной по чисто физическим соображениям. Однако в общем случае для этого требуется прибегнуть к какому-либо критерию устойчивости, проверив условия устойчивости в произвольной точке каждой из этих областей, пока не найдется область устойчивости.

У приведенной на рис, 4-6, г области устойчивости линии 1, 2 и 3 соответствуют первому, второму и третьему уравнениям (4-10), Эти линии разбивают плоскость к, Т на ряд областей, из которых в данном случае, несомненно, областью устойчивости является область, включающая положительную полуось Г поскольку точки этой полуоси соответствуют коэффициенту передачи системы к = 0. Последнее предопределяет устойчивость системы, так как она состоит из устойчивых звеньев.

По критерию Михайлова система находится на границе устойчивости, когда годограф D (/со) = С/в (w) -f jVd (со) проходит через начало координат. Таким образом, уравнения границы устойчивости в пространстве варьируемых параметров А и В, согласно этому критерию, имеют вид:

Ud {А, в, со) = 0; Vd{A, в, о)) = 0.

(4-11)

Эти уравнения, разумеется, включают все три названных выше случая попадания системы на границу устойчивости. Нулевой корень прп этом соответствует ю = О, а бесконечный со = оо.

Исключив из уравнений (4-11) параметр ю, можно получить уравнение границы устойчивости, связывающее входящие в выражения Ud (А,В,а)) и Vd {А,В,о)) варьируемые параметры А и В. Однако практически проще строить границу устойчивости,

используя со как параметр, который изменяют от О до оо. Каждо.му значению со при этом соответствует определенная точка границы устойчивости.

При некоторых значениях со может оказаться, что система (4-11) превращается в одно уравнение, которое даст на плоскости А, В линию. Такие линии называются особыми л и н и я м и. В случае построения области устойчивости, изображенной па рнс. 4-6, г, с помощью кргггерия Михайлова такими особыми линиями являются прямые 2 и 3. Первая из них соответствует со = 0, а вторая, со = .со. Линпя 1 соответствует конечным значениям со, причем вдоль нее со увеличивается при двин;ении в сторону уменьшения 1\.

После нрстроенпя линий, соответствующих уравнениям (4-11), надо по-пре;кнему из всех областей, на которые они разбивают нространство варьируемых параметров, найти область устойчивости.

В сиучае нримененпя критерия Михайлова последнюю операцию можно упростить, воспользовавшись специальной методикой, позволяющей сразу указать ту единственную область, которая может претендовать на то, чтобы- быть областью устойчивости. Если проверка на устойчивость в произвольной точке этой области дает отрицательный результат, это означает, что во всем рассматриваемом пространстве варьируемых параметров область устойчивости вообще отсутствует.

Упомянутая специальная методика заключается в следующем правиле нанесения штриховки на построенные по уравнению (4-11) линии. Предварительно составляется определитель

Каждая линпя штрихуется слева при движении по ней в сторону увеличения со, если знак определителя Д при значениях варьируемых параметров, соответствующих точкадг этой лпшш, положителен, и справа - в противном случае.

После нанесения таким образо.м штриховки на все линии областью, претендующей на то, чтобы быть областью устойчивости, будет область, в сторону которой обращены штриховкой все ограничивающие ее линии.

При этом, поскольку вдоль особой линии величина со не меняется, особые линии штрихуются в зависимости от направления штриховки основных, т. е. неособых, линий, с которыми они имеют общие точки, включая ххождение их в бесконечности. Особые линии штрихуются только в случае, если в таких общих точках онределите.иь Д меняет знак. Они штрихуются тогда навстречу основным линиям. (В результате, в зависимости от наиравлення

щтрихОБКи основных ЛИНИЙ, штриховки особых и основных линий получаются нанравленными либо друг к другу, либо, наоборот, п противоположные стороны.) Для иллюстрации на рис. 4-6, д показано.нанесение штриховки по этому правилу для ранее приведенного на рис. 4-6, г примера. Как видно из рис. 4-6, д, основ-Н1.те липни, на которых со изменяется, штрихуют двойной штриховкой.

Методика построе?шя областей устойчивости на основе критерия Михайлова, включая описанный вьпне метод штрпховки, разработана советским ученым Ю. И. Неймарком п получила назва-н-ие метода Z) - р а з б и с н и я.

Согласно критерию Найквиста, уравнения, определяющие границу устойчивости, имедот вид:

U,v{A, В, со) = -1; Vw{A, В, со)-О,

(4-12)

где Uw и Vw - действительная и мнимая частп (/со). Эти уравнения соответствуют прохождению а. ф. ч. х.-W Цы) через точку (- 1, /0).

Уравнения (4-12) приводят к тем же параметрическим выражениям, что и уравнения (4-10), полученные пз критерия Михайлова.

ГЛАВА ПЯТАЯ

КАЧЕСТВО ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

§ 5-!. ПОНЯТИЕ О КАЧЕСТВЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ

К процессам управления предъявляются следующие три основных требования: по точности в установившихся режндгах, по устойчивости и по качеству переходных процессов. Точность в установившихся режимах и устойчивость САУ рассмотрены выше. Перейдем теперь к расслготрению качества переходных процессов в САУ. .

Устойчивость САУ, т. е. затухание переходных процессов в Hcii, является необходимым, но далеко не достаточныд! условием практической пригодности системы. Существвпно еще качество переходных процессов, т. е. сам характер протекания переходных процессов и прежде всего пх длительность и колебательность.

На рис. 5-1 приведены примеры переходных характеристик САУ, представляющих собой переходные процессы на выходе системы, вызванные воздействием в виде единичного скачка