Рассмотрим в качестве примера систему третьего порядка, состоящую из трех статических звеньев первого порядка. Передаточная функция этой системы имеет вид:

W(n) = i

(см., например, систему на рис. 1-19). В этом случае

Dik) = R (Х) + Qik) = к,к,к, + {Т,Х + 1) {Т,Х + 1) {Т,к -Ь 1),

(4-8)

т. е.

D (X) = йдЯз + 12 + йоХ + йз,

(4-8а)

причем k=kjck.

Условие устойчивости, как показано выше, для п - Ъ сводится к следующим неравенствам:

k+iyO,

Oi 2 - о з = (12 + 2?з + 3i) (1 + Ta + з) -

-T,TJ,{i+k)>0.

Первые три неравенства не представляют интереса, если мы ограничиваем рассмотрение положительными значениями постоянных времени.

Следующее, четвертое, неравенство налагает ограничение на отрицательное значение коэффициента передачи к. Абсолютное значение к при этом должно быть меньше единицы. Практически зто неравенство тоже не имеет значения, показывая только, что система теряет устохшивость при неправильном замыкании обратной связи, когда она будет положительной, а не отрицательной, т. е. когда к < i. (В § 1-5 показано, что изменение знака обратной связи приводит к изменению знака W в знаменателе W.)

Реальные ограничения на значения параметров системы налагает последнее неравенство (4-8а). Его удобно неренисать в таком

виде: /4 1 -1 \

к<{Т, + Т, + Т,)(-ф- + + -1. (4-86)

Это неравенство показывает, что при любых значениях постоянных времени устойчивость системы нарушится при неограниченном увеличении коэффициента передачи к системы. Предельное по устойчивости значение к определяется постоянными времени системы. Согласно (4-86), это критическое значение

кр = (?х+72 + з)( + +5)-1.

(4-8в).

§ 4-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА

Это графический критерий. Он предложен в 1938 г. советским ученым А. В. Михайловым и тоже основан на рассмотрении многочлена D {X).

Подставим в этот многочлен вместо X мнимую переменную /со. В результате получим комплексную функцию

Здесь Ud (w) - действительная часть, полученная из членов D (?i), содержащих четные степени X, а Vq (со) - мнимая часть, полученная из членов D (Х) с нечетными степенями X. .

Изобразим D (/и) в виде годографа в комплексной плоскости (кривая 1 на рис. 4-3, а). Этот годограф называется годографом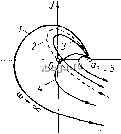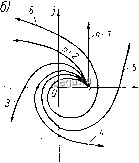

Рпс. 4-3. К критерию устойчивости А. В. Михайлова.

Михайлова. Каждому значению со соответствуют определенные значения 11 ( ) и Vd ( ) и определенная точка на плоскости. При 0) = О функция D (70)) = й , т. е. годограф начинается на действительной оси. При со оо функция D (;со) тоже неограниченно возрастает.

Критерий Михайлова формулируется так: система устойчива, если годограф D (/со), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно п квадрантов, где п - порядок системы.

На рис. 4-3, а годограф 1 относится к устойчивой, а годографы 3, 4 ж 5 - к неустойг}ивым системам.

Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова- через начало координат (кривая 2 на рис. 4-3, а). Действительно, в этом случае существует значение со, при котором D (/со) = О, т. е. характеристическое уравнение системы имеет пару сопряженных мнимых корней к ~ ±;со. Последнее и означает наличие в системе незатухающих колебаний, т. е. нахождение ее на границе устойчивости.

Незначительное изменение параметров системы, в результате чего годограф D (/со) на рис. 4-3, а отойдет влево от начала координат, делает систему устойчивой, а изменение параметров в другую сторону - неустойчивой.

На рис. 4-3, б приведены годографы устойчивых систем разных порядков до п = 6.

При построении годографа D (/со) прежде всего находят точки его пересечения с координатными осями. Для этого, определив из уравиенпя

значения частот, соответствующих точкам пересечения годографа D {](Х))с йптмон осью, подставляют их в выраич-ение (со). В результате получают соответствующие ординаты. Аналогично находят точки пересечения D (/со) с действительной осью, приравнивая нулю мнимую часть . (со).

Чтобы ие иметь дело с высокими степенями со, построение годографа D (;оз) можно производить по звеньям системы. Представим D {]ы) таким образом:

D (/со) = R (/со) + Q (/со) = П Л. (/со) + П <?г (/ ), (4-9)

где R- (/ю) и (/со) - числитель и знаменатель амплитудно-фазовой частотной функции i-ro звена приведенной одноконтурной системы.

Согласно выражению (4-9), построение годографа D (/со) начинают с построения годографов R- (/со) и Q- (/оз) отдельных звеньев. Затем строят годографы i? (/со) и Q (/со) путем перемножения соответствешю годографов /? (/со) и Q- (/со). Годографы перемножают по обычным правилам перемножения векторов, как и при построении частотных характеристик цепочки звеньев по характеристикам отдельных звеньев (см. § 1-5). Для каждого значения со модули (величины векторов, проведенных из начала координат в соответствующую точку годографов) перемножают, а аргументы (фазы этих векторов) складывают.

Заметим при этом, что для обычных типовых звеньев, исключая диффере1щирующие, Л;Д/оз) равны просто коэффициенту передачи звена и соответственно у систели.1, состоящей из таких звеньев, годограф R (/со) = /с, т. е. вместо его построения для получения годографа D (/со) достаточно просто сдвинуть ранее построен--нып годограф Q (/со) вправо па величину к.

§ 4-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА

Этот критерий, предложенный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по амплитудпо-фазовой частотной характеристике (а. ф. ч. х.) W (/со) разомкнутой системы (рис. 4-4, а).

Сформулируем сперва этот критерий для случая, когда известно, что система в разомкнутом, состоянии устойчива. Условие устойчивости замкнутой системы тогда сводится к требованию, чтобы а. ф. ч. X. разолгкпутой системы не охватывала точку (-1, /0).

На рис. 4-4, а характеристики 1 п 4 соответствуют устойчивым С!гстемам, характеристика 5 - неустойчивой, а характеристика 2- иахождеиию системы иа границе устойчивости. Если, например, уменьшить коэффициент передачи в неустойчивой системе, се а. ф. ч. X. сожмется к началу координат, в результате чего система станет устойчивой.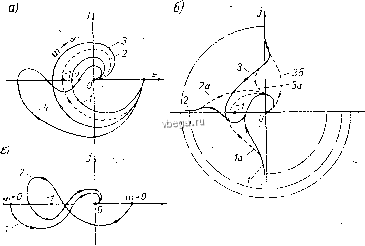

Рис. 4-4. К критерию усто11Ч1[вости Г. Найквиста.

Наоборот, при увеличении коэффициента передачи характерп-CTTfKa устойчивой.системы в конце концов охватит точку (-1, /0) и система потеряет устоГчивость.

Амплитудно-фазовые характеристики, показанные на рис. 4-4,о, принадлежат статическим сис1темам. На рис. 4-4, б приведены а. ф. ч. X. астатических систем с разным порядком астатизма. Кривые 1, 2 и 3 относятся к системам соответственно с астатткз-мо.м 1, 2 и 3-го порядков. А. ф. ч. х астатических систем при со = О уходят в бесконечность, так как в знаменателе амплитудно-фазо-Boit функции W (/со) имеется множитель (/Чо) , где г - порядок астатизма. Соответственно, как показано па рис. 4-4, б, при г - 1 характеристика W (/со) при со = О уходит в бесконечность вдоль отрицательной мнимой полуоси, при = 2 - вдоль отрицательной действительной полуоси, а при / = 3 -- вдоль положительной мнимой полуоси. Для сулчдения об устойчивости астатической системы находящееся в .бесконечности начало ее а. ф. ч. х., соответствующее со = О, надо мысленно соединить с положительной

действительной полуосью против часовой стрелки дугой бесконечного радиуса, как условно изобрая?ено иа рис. 4-4, б штрих-пупк-тирными линиями. В случае устойчивой системы точка (-1, 7О) пе должна охватываться а. ф. ч. х., мысленно дополненной дугой, соединяющей ее с положительной действительной полуосью. Сказанное иллюстрируется на рис. 4-4,6. Пунктирные кривые 1а, 2а и За {36) соответствуют неустойчивым системам с астатиз-мом 1, 2 и 3-го порядков. .

Как было указано, данная выше формулировка критерия Найквиста относится к системам, которые являются устойчивыми в разомкнутом состоянии. В случае одноконтурной системы устойчивость в разомкнутом состоянии всегда обеспечивается, если система состоит только из устойчивых звеньев. При наличии местных обратных связей должна быть еще проверена устойчивость образованных этими связями контуров. Для этого, в свою очередь, может быть применен критерий Найквиста или любой другой.

Для систем, неуст011чивых в разомкнутом состоянии, критерий Найквиста имеет такую формулировку: для устойчивости системы в замкнутом состоянии а. ф. ч. х. разомкнутой системы должна охватывать точку (-1, /0). При этом число пересечений ею отрицательной действительной полуоси левее точки (-1, уО) сверху вниз должно быть на /с/2 больше числа пересечений в обратном направлении, где к - число полюсов передаточной функции W (р) разомкнутой системы с положительной действительной частью.

На рис. 4-4, в в качестве примера показаны две а. ф. ч. х. разомкнутой системы, неустойчивой в разомкнутом состоянии вследствие наличия правых корней, но устойчивой в замкнутом состоянии.

Характеристика 1 соответствует /с = 1, а характеристика 2 - значению /с = 2. ,

Таким образом, в общем случае при применении критерия Найквиста необходимо предварительно определить число правых полюсов ТУ (р). Для одноконтурной системы, когда знаменатель W (р) представляет собой произведение знаменателей передаточных функций отдельных звеньев, это число находится легко, поскольку полюсами W (р) являются полюсы передаточных функций звеньев.

У многоконтурных систем, особенно с перекрестными связями, задача определения числа к усложняется, и поэтому в этих случаях целесообразно отказаться от применения критерия Найквиста.

\/В соответствии с критерием Найквиста об устойчивости можно судить не только но а. ф. ч. х., но и совместно по а. ч. х. и ф. ч. х. разомкнутой системы. Обычно при этом пользуются логарифмическими характеристиками, что представляет большое удобство в силу простоты их построения.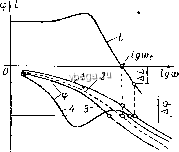

Согласно критерию Найквиста, для системы, устойчивой в ра-30MiaiyT0M состоянии, условием устойчивости ее в-замкнутом состоянии является неохват а. ф. ч. х. ТУ (/со) точки (-1, /0). Последнее имеет место, если при частоте, на которой А (со)= 1, фаза ср (со) > - . t, т. е. абсолютное значение фазы меньше л.

Сказанное непосредственно следует из рис. 4-4,-а.

Таким образом, применительно к логарифмическим характеристикам, если учесть при этом, что значению Л = 1 соответствует L 20 Ig Л = О, критерий устойчивости Найквиста для спстем, устойчивых в разомкнутом состоянии, сводится к тому, что л. а. х. должна пересечь ось абсцисс раньше, чем фаза окончательно перейдет за значение - я. Или иными словами: на частоте среза величина фазы должна быть меньше л.

Изложенное иллюстрируется рис. 4-5. Здесь изображены л. а. X. L (со) и четыре варианта л. ф. X. ср (со). В случае л. ф. х. 1 и 4 замкнутая система устойчива, причем характеристика 4 соответствует а. ф. ч. X. 4 на рис. 4-4, а. Л. ф. X. 2 соответствует нахождению замкнутой системы на границе устойчивости, ал. ф. х. 3 - неустойчивой замкнутой системе.

Для астатических систем и систем, неустойчивых в разомкнутом

состоянии, требования к л. а. х. и л. ф. х. в отношении устойчивости можно сформулировать, исходя из соответствующих требований к а. ф. ч. X. В частности, для систем, неустойчивых в разомкнутом состоянии, условием устойчивости в замкнутом состоянии яв.пяется следующее: при положительной л. а. х. число пересечений л. ф. х. уровня - л снизу вверх должно быть на к/2 раз больше числа пересечений в обратном направлении.

При оценке устойчивости систем одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т. е. степени удаленности системы от границы устойчивости. Система, которая теоретически является устойчивой, но находится очень близко к границе устойчивости, практически при ее реализации может оказаться неустойчивой как вследствие неточнос;ти математического описания системы, использованного при оценке устойчивости, так и из-за изменения во времени параметров системы.

В- случае применения критерия Рауса - Гурвица о запасе устойчивости можно судить по тому запасу, с которым выполняются входящие в этот критерий неравенства. При использовании графических 1чритериев Михайлова и Найквиста запас устойчивости определяется удаленностью соответствующих характеристик

Рис. 4-5. Логарифмическ1П1 критерий устойчивости Г. Найквиста.