Взаимная корреляционная функция обладает теми же свойствами, что и корреляционная (автокорреляционная) функция. Если процессы х (t) и ij (t) статистически независимы и хотя бы один из них центрирован, R (т) = 0.

Спектральная плотность. Снектральная плотность S{(i>) случайного процесса х (t) - это частотная функция, характеризующая спектральный (частотный) состав процесса. В отличие от ранее введенных частотных функций, спектральная плотность представляет собой частотную функцию для средних значений квадратов амплитуд гармоник, па которые может быть разложен случайный процесс.

Поскольку мощность гармонического сигнала пропорциональна квадрату его амплитуды, спектральную плотность случайного процесса можно физически трактовать как частотную функцию, определяющую распределение среднего значения мощности процесса по спектру, т. е. по гармоникам. Поэтому ее часто называют спектральной плотностью мощности.

Для стационарного случайного процесса х (t) формально спектральная плотность (со) может быть получена как изображение Фурье корреляционной функции:

(3-21)

Функция i?, (т) является четной функцией т, т. е.-/?, (-т) = = /?, (т). Поэтому выражение (3-21) удобно представить в тригонометрической форме:

/5 , (о)) = 2 i? (т) cos т dx.

(3-22)

Последнее выражение получается после подстановки в (3-21)

е~ i = cos о)т - /sin о)т

и отбрасывания мнимой части полученного выражения в связи с тем, что 5, (ш) является действительной функцией.

С помощью обратного преобразования Фурье можно выразить корреляционную функцию через спектральную плотность:

(3-23)

или в тригонометрической форме, учитывая, что (w) - четная функция:

в соответствии с (3-14) из (3-23) вытекает следующее выраже-

ние:

ш со

RAO) = ± Л(о))йа) = -1 \ 5,(co)rfa). (3-25)

Это выракение для среднего значения квадрата случайной функции X {t) через спектральную плотность очевидно, поскольку представляет собой интегрирование по средним значениям квадратов амплитуд гармоник случайного процесса х (t).

в случае центрированной случайной функции из (3-25) вытекает следующее важное выражение для дисперсии:

со со

D=[x(t)\= 5,o(a))rfo)= S,o(a))6/w. (3-26)

- со о

На рис. 3-4 показаны графики спектральной плотности, соответствующие различным корреляционным функциям. Соотноше-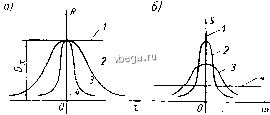

Рпс. 3-4. Корреляционные функции и спектральные плотности центрированных стационарных случайных процессов.

нпе между спектральной плотностью S (о)) и корреляционной функцией R (т) здесь аналогично рассмотренной выше связи между обычной частотной и переходной характеристиками: чем шире график корреляционной функции, тем уже график спектральной плотности, и наоборот.

в предельном случае, соответствующем кривым 1, когда х (t) представляет собой детерминированную постоянную величину а, корреляционная функция тоже постоянна и равна D, = [см. выражение (3-15)]. В этом случае спектральная плотность существует только при нулевой частоте и, согласно (3-22), равна 2л(w).

В другом предельном случае, соответствующем кривым 4, X (t) является чисто случайным стационарным процессом, когда связь между последующими значениями х {t) совсем отсутствует. Такой случайный процесс называется белым шумом. Его корреляционная функция нропорциональна дельта-функций, т. е.

где а = const.

Согласно (3-22), соответствующая спектральная функция S (со) = а = const.

Случайный процесс в виде белого шума практически невозможен, так как имеет бесконечный спектр и соответственно бесконечную мощность. Однако реальные случайные процессы с конечным спектром часто можно ириближенно представить в виде белого шума, если рассматривается действие их на систему, полоса пропускания которой значительно же ширины спектра процесса. В част-иости, именно так обычно представляют тепловые шумы в усилителях. ,

По поводу характера кривых R (т) и 5 (со), изображенных на рис. 3-4, отметим, что разные максимумы кривых S (со) при одинаковых максимумах соответствующих им кривых R (т) объясняются тем, что илощадн под кривыми S (со), согласно (3-26), пропорциональны дисперсии случайного процесса, т. е, максимуму R (т).

В качестве частотной характеристики статистической связи между двумя стационарными случайными процессами х {t) и у (t) применяется взаимная снектра.льная плотность, представляющая собой изображение Фурье взаимной корреляционной функции:

(3-27)

§ 3-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПРИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

Стационарные случайные воздействия / {t) вызывают соответственно стационарные случайные изменения выходной величины X {t) системы автоматического-уиравления (если последняя, разумеется, тоже стационарна). Найдем связь между характеристиками процессов / (t) и X (t) на входе- и выходе системы.

В общем случае случайное воздействие / {t) состоит из среднего значения {t) и центрированной случайной части / {t), т. е.

Соответственно может быть представлена и выходная величина системы: x{t) = mjt)+x<{t).

Для линейной системы на основании принципа суперпозиции каждая из этпх двух составляющих х {t) может быть определена порознь: Шд. (t) - как реакция на 7?? (t), а х (t) - как реакция .на /о (О-

Средние значения тп {t) и {t) являются неслучайными величинами и связаны через передаточную функцию системы, т. е.

mJi) = W,{p)mj{l). (3-28)

В частности, для стационарного случайного процесса /Пу (t) и соответственно (t) представляют собой постоянные величины. Поэтому связь между ними определяется по уравнению статики системы, как. показано в § 2-2, т. е.

т, = Жз (0)ту.

(3-29)

Перейдем теперь к определению центрированной стационарной случайной величины ж {t) по {t).

Входное воздействие/ (t) может быть задано либо корреляционной функцией Rfo (т), либо спектральной плотностью 5/ (со). Эти характеристики могут быть получены, в частности, в резуль-, тате обработки экспериментально снятых кривых / (t).

Выходная величина ж {t) также может быть охарактеризована функциями Rx (т) или Sx (со).

Определим связь между корреляционными функциями и спектральными плотностями на входе и выходе системы. Начнем с кор-. реляционных функций.

Чтобы получить искомое выражение для корреляционной функ-. цип выходной величины

R,(T) = M[xit)xit+x)\

по корреляционной функции входного воздействия, воспользуемся связью между входной и выходной величинами системы через, ее весовую функцию w (t). Согласно (1-ЗОа),

X (t) =\w (Tl) f (t - j) d-c.

(З-гоу

Перепишем это выражение для х {t + х), введя новую независимую, переменную

с . .

xit + T)=w (тз) / ( + т - Та) dx. Тогда входящее в R. (т) произведение

оо оо

X{t)xit + X)=\ W (Tl) / {I - Tl) rfXi \ W (Та) f{t+x - x)dx, dx

oo oo

= П (Tl) w (Та) / (г - Tl) / (< -Ь T - Та) cTi dx.

Отсюда корреляцпонная функция как среднее значение этого-выражения

оо со

R{x)=\\w (Tl) w (Та) (т 4- Tl - Та) dx dx. (3-31)= о о

Получили искомое выражение, связывающее i?, (т) с Rf {%) через весовую функцию w {t) системы. Чтобы пояснить смысл этого выражения, представим его в следующем виде:

г/ (т) = 5 (i) Рч (т + tJ cTi.

(3-32)

Отсюда видно, что корреляционная функция R (т) процесса на выходе системы получается двукратным взятием интеграла Дюамеля (интеграла свертки) от корреляционной функции R (т) входного воздействия.

Выражения (3-31) и (3-32) определяют связь между Rf (т) и R (т) в интегральной форме. Ее можно представить и в дифференциальной форме через передаточную функцию системы в следующем виде:

К i-) = ip) V, (- Р) Rf (т). (3-33)

Это вьфажение неносредственно вытекает из (3-32), так как интегральной зависимости (3-30) между входом и выходом системы эквивалентна зависимость через передаточную функцию:

x{t) = W, {p)f{t).

Соответственно двукратной зависимости (3-32) эквивалентно произведение передаточных функций в выражении (3-33). Передаточная функция Из (-р) соответствует второму уравнению (3-32), где по сравнению с выражением (3-30) вместо т стоит -т. Формально это означает изменение направления течения времени и, следовательно, изменение знака у производных, т. е. знака оператора р в соответствующей передаточной функции.

Выведем теперь выражение, связывающее спектральные плотности входной и выходной величин системы, т. е. рассмотрим связь между частотными характеристиками этих сигналов.

Для этого подставим найденное выше выражение (3-33) для R (т) в формулу (3-21) для (со), т. е. проведем над этим выражением преобразование Фурье. В результате получим

(0)) = W, (/со) W, (-/со) 5/ (со) = I PF3 (/со) 2 S, (со), (3-34)

, 6,(co) = yl( )5/((o).

Таким образом, спектральная плотность стационарного случайного процесса на выходе системы равна спектральной плотности входного воздействия, умноженной на. квадрат амплитудной частотной функции системы.

Собственно, формула (3-34) очевидна и из чисто физических представлений, если учесть, что амплитудная частотная функция определяет отношение амплитуд колебаний на выходе и входе сп-

сте1пл, а спектральная плотность есть частотная функция для средних значений квадратов амплитуд гармоник.

Рассмотрим теперь более общий случай, когда к системе одновременно приложены в разных точках два стационарных случайных сигнала {t) и /2 {t).

На основе принципа суперпозиции в этом случае вместо (3-30) имеем

со оэ

ж (О = S (Tl) /1 [t - Tl) с/т, -Н \ (т,) /2 [t - Tl) c/ti.

Здесь 11 и Wo, - весовые функции системы для воздействий Д и /2 соответственно.

Написав, как и ранее, выражение для произведения х (t) х X X {t т) и усреднив его, получим следующее выражение для корреляционной функции выходной величины:

со со

() = \\[Щ Щ Ы ( + Tl - Т2) +

+ (Т.) W.2 (Tl) Rff (т + Tl - Т2) + IV, (Tl) 2 (T2) (Т + Tj - Тг) -}-

-f (Ti) iv (Tj) Rf (t + Tl - T2)] cTi dx. (3-35)

Здесь Rij и - взаимные корреляционные функции; в об-

щем случае они не равны друг другу.

Совершив над полученным выражением преобразование Фурье, получим в соответствии с (3-33) следующее выражение для спектральной плотности на выходе системы:

( ) = Wsi (/ ) (-/со) Sf (w) + IF31 (/(О) IF32 (-/со) S,j (со) + + Из2 (/ ) 31 (-/ ) /J, (со) + VK32 (/со) (-/со) Si (со). (3-36).

Здесь и Из2 - передаточные функции системы для воздействий /1 и /2.

Если случайные функции Д (t) и /2 {t) взаплпю независимы и хотя бы одна из них является центрированной, их взаимные корреляционные функции и взаимные спектральные плотности обращаются в нуль, и формулы (3-35) и (3-36) принимают более простой вид:

(г) = И i (1) 1 ( 2) (т -Ь т, - Тг) rix, dx., +

со со

+ \ \ 2 (Tl) г2 (Т2) (т + Tl - То) dx dx; (3-35а>

Здесь

(0)) = (со) S, (0)) + Al, (со) Sf (со). 31 Н = I lai (/ ) I; А3., (о>) = I (/03) 1.

(3-36а)