функцию р (х) называют также дифференциальным законом распределения случайной величины. Слгьтсл этого названия очевиден из определения функции р (х) согласно (3-2).

Вместо р (х) непрерывную случайную величину можно характеризовать еще так называемым интегральным законом распределения F {х). Величина F {х) представляет собой вероятность того, что случайная величина х примет значение меньше некоторого Xj, т. е.

Г{х) = Р{х<:х,)= \ p[x)dx.

(3-5)

Примерный график F [х) показан на рис. 3-1, в.

При статистическом описании реальных случайных величин их стараются свести к одному из типовых законов распределения аналогично тому, как реальные детерминированные воздействия стремятся сводить к каким-либо типовым воздействиям (ступенчатому, гармоническому, линейно возрастающему и т. п.). Такими типовыми законами распределения являются распределение Гаусса, илп нормальное распределение, равномерное распределение, распределение Пуассона (для дискретных случайных величин), распределение Релея, Коши и др. Основное распространение в системах автоматического управления имеет нормальное распределение. Примером такого распределения является распределение, показанное на рис. 3-1, б. Практически можно считать, что всякая непрерывная случайная величина, представляющая собой результат действия достаточно большого числа независимых случайных причин, имеет нормальное распределение. Например, ошибка при стрельбе.

На рис. 3-1, г изображено равномерное распределение. (Здесь любое из возможных значений х равновероятно.) Такое распределение имеет, например, величина отклонения (ошибка), вызванного зоной нечувствительности измерительного прибора, исполнительного устройства и т. п.

На рис. 3-1, а показано распределение Пуассона. Различные законы распределения описаны в работе [6].

Если случайная ве,дпчина х характеризуется законом распределения р (ж), то у случайного процесса закон распределения р {х, t) является функцией времени. Каждому конкретному моменту времени соответствует свой закон распределения. В случае стационарного случайного процесса закон распределения не меняется во времени, т. е. р [х, i) = р (х). Однако, если для случайной величины закон распределения р (х) является исчерпывающей ее характеристикой, то для стационарного случайного процесса, помимо закона распределения р (х), необходимо знать еще быстроту протекания его во времени, т. е. его временные или частотные свойства. (Действительно, закон распределения р (х) стацио-

парного случайного процесса не зависит от масштаба времени, в то время как изменение последнего означает изменение быстроты протекания процесса.) Для характеристики этой стороны случайного процесса применяют особые функции - корреляционную функцию и функцию спектральной плотности, которые будут даны несколько ниже.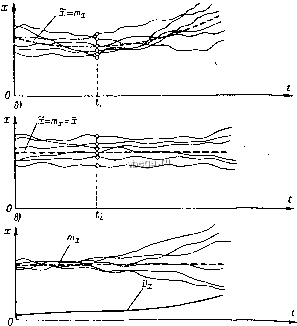

Рпс. 3-2. Случайные nj)ou,ecci.i.

Среднее значение. Среднее значение случайной величины ж, определенное по множеству ее возможных значений и называемое еще математическим ожиданием ж.

= М \х\ = хр (ж) dx.

(3-6)

Среднее по множеству обозначается также в виде х.

Для дискретной случайной величины интеграл в (3-6) превращается в сумму всех дискретных значений величины, умноженных на их вероятности.

Для случайного процесса х (t) величина (t) является функцией времени (рис. 3-2, а). Однако, если случайный процесс стационарный, то у него постоянно во времени (рис. 3-2, б).

Для стационарного случайного процесса практически всегда может быть принята гипотеза о его эргодичности.

Свойство эргодичности заключается в том, что среднее по множеству равно среднему по времени. Среднее по времени - это среднее значение функции, определенное для отдельной реализации случайного процесса х [t) (для отдельной кривой на рис. 3-2). Оно обозначается X и согласно определению

х= lim \ x{t) dt.

(3-7)

В отличие от среднего по времени, среднее по множеству х для случайной функции х (t) определяется для каждого момента времени (рис. 3-2, а и б) путем усреднения по всем реализациям процесса (по всем кривым рис. 3-2, а и б). Из чисто физических представлений эргодичность стационарного случайного процесса очевидна. Действительно, поскольку вероятностные характеристики стационарного случайного процесса не меняются с течением времени, длительное наблюдение за отдельной реа.тизацией такого процесса на одном объекте должно дать в среднем ту же картину, что и наблюдения, сделанные в один п тот же момент на большом числе одинаковых объектов.

Свойство эргодичности сильно упрощает экспериментальное определение вероятностных характеристик стационарных случайных процессов, поскольку позволяет заменить эксперимент на большом числе объектов экспериментом на одном из них, правда, в течение достаточно длительного времени п, соответственно, статистической обработкой одной реализации случайного процесса.

Таким образом, для стационарного случайного процесса благодаря его эргодичности среднее по множеству х, т. е. математическое ожидание т, можно определять как среднее по времени х:

со Т

m,M[x{t)]= xpix)dx = lim x{t)dt. (3-8),

-со Т со

Случайная функция (и величина), мате>штическое ожидание которой равно нулю, называется центрированной. Соответственно, случайную функцию можно представить как сумму математического ожидания и центрированной случайной функции, т. е.

xit) = m,it) + x{t). (3-9)

Здесь через х° (t) обозначена цснтрп.роваппая случайная функция.

Дисперсия и среднеквадратичное отклонение. Дисперсия случайной величины х - это среднее значение квадрата ее отклонения от среднего значения:

= М [{X - т,Г] =3 {х- ш,)р(X) dx

(3-10)

или с учетом (3-9)

0,М\{х)]= \ (xrp(x)dx,

(З-Юа)

где ж - центрированная часть случайной величины х.

Дисперсия является мерой отклонения случайной величины х от ее среднего значения. Чем больше флуктуации случайной величины относительно среднего значения, тем больше дисперсия. Последнее иллюстрируется рис. 3-2, в.

Для стационарного случайного процесса, основываясь на свойстве эргодичности, дисперсию можно определить усреднением во времени:

i), = vV/{[a: (/)n=IV7)p = lim 2 [ {xiOfdt. (3-11)

Среднеквадратичное отклонение

(3-12)

Эта величина часто используется вместо в .качестве меры отклонения случайной величины. Она удобна тем, что имеет ту же размерность, что и сама случайная величина, в то время как дисперсия имеет размерность квадрата случайной величины.

Корреляцпонные функции. Эти функции служат для количественной оценки зависимости между последующими во вре.мснп значениями случайного процесса, т. е. оценивают быстроту изменения случайного процесса во временп.

Корреляционная (или автокорреляционная) функция Ry. (т) случайной функции х [t) - это среднее значение произведения двух значений этой функции, сдвинутых на определенный промежуток времени т, т. е.

(3-13)

R,ix) = M[x{t)xit+x)].

В случае стационарного случайного процесса, используя свойство эргодичности, корреляционную функцию можно определить как среднее значение по времени:

/?(т)==ж(Ож(/ + т)= lim [ xit)x{tx)dt. (3-13а)

При этом практически значение корреляционной функции стационарного случайного процесса может быть найдено по достаточно длинной записи случайного процесса путем вычисления интеграла от произведения текущего значения функции на ее значение, сдвинутое во времени на т (рис. 3-3, а). Корреляционные функции вычисляются обычно с помоьхью специальных приборов, называемых корреляторами [7].

На рис. 3-3, б показан типичный вид корреляционной функции. С ростом т корреляционная функция убывает. Это отражает ослабление влияния (корреляции) на текущее значение случайной функции ее предыдущего значения при увеличении сдвига по вре-.мени между ними. Любой реальный объект, в котором происходит интересующий нас случайный процесс х (t), обладает определенной инерционностью. Вследствие этого случайный процесс не может изменяться бесконечно быстро, т. е. текущее значение случайной функции х (t) не является совершенно независимой случайной величиной, а в какой-то степени в среднем зависит

ti+X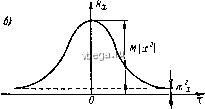

Рпс. 3-3. Корреляцпонная функция стационарного случайного процесса.

от предшествующих ее значений или, как говорят, коррелировано с ними.

Корреляционная функция служит мерой этой зависимости, поскольку ее значение, определенное по формуле (3-13), будет тем больше, чем меньше посшдующее значение данной случайной функции X [t -\- х) в среднем отличается от ее текущего значения X (t). При этом максимальное значение корреляцпонная функция имеет при т = О, когда х (t -\- х) = х (t) и, согласно (3-13), это значение Я, (0) равно среднему значению квадрата случайной функции, т. е.

RAO) = M[x]. (3-14)

Очевидно, такому же значешш будет равна корреляционная функция при всех значениях т для детерминированной постоянной во времени величины а, т. е.

HJx)=:a\

(3-15)

Для случайного же процесса с ростом т корреляционная функция убывает соответственно тому, как увеличивается при этом в среднем отклонение х (t -\- х) от х (t).

Тот факт, что всегда

/?,(T)i?,(0),

легко доказать для стационарного случайного процесса исходя из неравенства

x{t) + xHt,)-2x{t,)xit,)0, которое является очевидным, поскольку его левая часть равна

Ь()-(УГ-

Перейдя к средним значениям путем определения математического ожидания, получим

М [2х (t,) X (t,)] М [ж (t,)] + М [х (t,)]. Отсюда, учитывая, что для стационарного случайного процесса М[хЦ1,)]=М[хЦ1,)]М[хЦ1)1

и подставляя 2 = + f, получаем в соответствии с (3-13) требуемое неравенство:

/?,(т)/?,(0) = Л/[ж=(0]. (3-16).

Значение корреляционной функции убывает с ростом т тем . быстрее, чем быстрее изменяется во времени случайный процесс X {t), поскольку при этом ослабляется связь между значениями х, отстоящими на фиксированный промежуток времени т.

Предельное значение корреляционной функции прп т = оо, как показано на рис. 3-3, б, равно квадрату среднего значения,.

i? (оо) = м:. (3-17)

Действительно, в бесконечно удаленные друг от друга моменты времени значения случайной функции х (t) можно считать независимыми и корреляционная функция будет отличаться от нуля, только за счет присутствия в этой случайной функции детерминированной постоянной составляющей в виде среднего значения тп, как это следует из (3-17).

Для центрированного случайного процесса

/?.,о(0)=--М{[ж (ОР}=А-с. (3-18)

а /?.,о(сх5) = 0, (3-19)

что следует непосредственно из выражении (3-14) и (3-17).

При рассмотрении двух случайных процессов х (t) т у (t) для оценки статистической связи (корреляции) между нилп! применяется так называемая взаимная корреляционная функция

R..,{x) = M[x{l)y{t + x)]. (3-20)