Установившееся значение Жут найдем по-прежнему подстановкой в это выражение для х значения р = О, т. е.

р=0 уст-

(2-10)

Из выражения (2-10) видно, что в статической спстелш, у которой W (0) = /с, а (0) = A,y, Жует оо при любом к из-за наличия множителя р в знаменателе, т. е. в статической системе при непрерывно возрастаюш,ем воздействии выходная величина х тоже непрерывно возрастает. Этот результат очевиден и из ранее полученного соотношения (2-2), согласно которому в статической системе установившееся отклонение х пропорционально воздействию.

Рассмотрим средства, с помош,ью которых можно ограничить п даже ликвидировать установившееся отклонение Жу при непрерывно изменяюш,емся воздействии. Как п в случае рассмотрения условий устранения установившегося отклонения в статическом режпме, здесь принципиально возможны два пути. Первый путь связан с выбором определенной передаточной функции разомкнутой системы IF (/?), стояш,ей в знаменателе выражения (2-10) для Жу,., а второй с выбором W(р) в числителе этого выражения. Как будет показано ниже, первый путь по-прежнему сводится к введению в систему интегрируюш,их звеньев, а второй - к ком-пенсацш! влияния возмущений. Рассмотрим последовательно эти пути.

Прпменеппе астатической системы управления. Пусть в общем случае в передаточную функцию разомкнутой системы IF (р) входит г интегрирующих звеньев, а в передаточную функцию VFy. (р) части этой системы - I таких звеньев. Тогда выражение (2-10) для установившегося отклонения х можно переписать так:

[1 + p-rW {р)\ ph

р=о=- P- + W(p)

р = 0

Ah) /уст-

Здесь, как и раньше, использована подстановка: IF (р)= W (р) и IF., (р) = p-IF;, (р), причем IF (0) = к, а IF;, (0) = к,.

Из приведенного выражения для Жу. следует, что при (г - I) =к установившееся отклонение х будет Ихметь конечное значение

- /уст-

(2-11)

Если (г - г) > к, значение хт = О, а при (г - I) </с величина X неограниченно возрастает со временем.

Выражение (2-11) более удобно представить в следующем виде:

f(h) уст

(2-11а)

где величина g = к/к называется добротностью. 74

Если значение Хут конечно при изменении воздействия с постоянной скоростью, т.е. когда = р/ = у, соответствующая добротность называется добротностью по скорости

п обозначается

ГГуцт

(2-116)

Добротность по скорости имеет разность 1/сек и численно равна скорости изменения воздействия, дающей единичное значение Жу.

Если Жуст конечно при изменении воздействия с постоянным ускорением, т. е. когда / = р-/ = а, соответствующая добротность называется добротностью по ускорению:

(2-11в)

Ее размерность 1/сев , и она равна постоянному ускорению, соответствующему Жуут = 1.

Как видно из приведенных формул, добротность системы пропорциональна коэффрщиенту передачи к.

Система, имеющая конечную добротность по скорости, является астатической, т. е. ее статизм равен нулю. В свою очередь, система, имеющая конечную добротность по ускорению, не имеет установившегося отклонения при изменении воздействия с постоянной скоростью, т. е. у нее = оо.

Количество интегрирующих звеньев в системе называется порядком астатизма системы. Если ввести еще понятие порядка воздействия, под которым надо понимать порядок фиксированной производной воздействия, то полученный результат можно кратко сформулировать так.

Если в IFy, (р) не имеется интегрирующих звеньев, установившееся отклонение Жут = О, когда порядок астатизма системы выше порядка воздействия, и Жу конечно и равно (2-11) в случае равенства этих порядков. Если W(р) содержит I интегрирующих звеньев, для получения тех же результатов надо порядок астатизма увеличить на I.

Таким образом, введение в систему определенного количества интегрирующих звеньев позволяет ограничить или совсем ликвидировать установившееся отклонение ж при наличии воздействия, непрерывно изменяющегося с постоянной производной.

Компенсация влияния возмущений, изменяющихся с постоян-Hoii производной. Выше при рассмотрении статического режима работы САУ был изложен способ устранения статического отклонения выходной величины объекта путем применения управ.тяю-щего воздействия по возмущению с целью компенсации естественного влияния этого возмущения на выход объекта.

Такая же компенсация может быть осуществлена и в стационарном динамическом режиме в отношении возмущений, изменяющихся с постоянной производной. Однако в отличие от компенсации в статическом релиме здесь управляющее устройство должно

действовать на объект в функции- не только самого возмущения, но и его производных.

В результате получается комбинированная система управления, показанная на рпс. 2-2, б. У этой системы

р = 0

/уст-

(2-12)

1 + W (р)

Определим вид передаточной функции управляющего ycTpoii-ства Wf (рУ по возмущению, при котором х,., обращается в нуль. Для этого рассмотрим числитель выражения (2-12), приведя его к общему знаменателю: \

[W,.Jp) + WJp)W,ip)\p =

Qf.iP)QliP)Qoip) t-o (Р) Qiu ip) Qo iP) + Rfu iP) (P) Qf.P) ] p- .

Здесь через R [p) я Q (p) с соответствующими индексалш обозначены числитель и знаменатель соответствующих передаточных функций.

Если рассматриваемая система является статической, все многочлены Q (р) при р-0 обращаются в единицу. Чтобы все полученное выражение при р = О обратилось в нуль, в выражении, стоящем в квадратных скобках, все слагаемые должны иметь р в степени выше порядка возмущения к. Это может быть обеспечено, если многочлен R (р) имеет вид:

/и (Р) = / о + IP + fP + + иУ- (2-13)

Действительно, многочлен R (р) Qf (р) (р) и многочлен /?о (р) QfXQ (Р) являющийся множителем у 7?, (р), включают члены с р в степени от О до величины, определяемой порядком этих многочленов. Если коэффициенты многочлена (р) сделать отрицательными, то несложно найти выражения для них через коэффициенты остальных многочленов, стоящих в квадратных скобках, по условию, чтобы все слагаемые многочленов Rfxo (Р) QfuiP) Qo (Р) и RfuiP) (Р) <?/.хо (Р) имеющие степень р . от о до к, взаимно уничтожились.

Многочлен Яу, (р) вида (2-13) означает, что управляющее устройство возде11Ствует-на объект в функции возмущения / и его к последовательных производных.

Таким образом, в статической системе при наличии возмущения, изменяющегося с постоянной скоростью, можно обеспечить Жург = О применением компенсирующих воздействий по этому возмущению и его первой производной. Для получения того же эффекта при возмущении, изменяющемся с постоянным ускорением, необходимо добавить воздействие по второй производной.

В астатической системе в зависимости от порядка астатизма и количества интегрирующих звеньев в передаточной функции Wf.{p) порядок производных от возмущения, которые должны измеряться управляющим устройством, соответственно увеличивается.

ГЛАВА ТРЕТЬЯ

СТАЦИОНАРНЫЕ РЕЖИМЫ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПРИ СЛУЧАЙНЫХ

ВОЗДЕЙСТВИЯХ

§ 3-1. ОСНОВНЫЕ ПОНЯТИЯ О СЛУЧАЙНЫХ ПРОЦЕССАХ

Для того чтобы наиболее точно исследовать поведение системы автоматического управления, необходимо прежде всего располагать как можно более точными данными о приложенных к системе воздействиях. Предельно точным описанием этих воздействий является задание их в виде детерминированных функций времени. Однако последнее далеко не всегда возможно либо по недостатку сведенш !, либо в связи с самой природой воздействия. В этих случаях воздействия на систему следует рассматривать как случайные функции времени и, соответственно, описывать их статистически.

Обратимся, например, к рассмотренной ранее системе автоматического регулирования напряжения генератора (см. рис. В-2). Основным внешним воздействием здесь является изменение нагрузки. Если нагрузка представляет собой достаточно большое число отдельных потребителей, время работы и мощность которых не могут быть заранее точно определены, будущее изменение такой нагрузки во времени может ыть описано только статистически на основе обработки ранее полученных опытных записей. Аналогичный случайньтй характер в этой же системе регулирования может иметь изменение напряжения питания цепи возбуждения генератора. Принципиально случайным по своей природе является возмущение в виде шума в усилителе регулятора.

Другими примерами случайных воздействий являются для автопилота воздействие ветра на самолет, колебания тяги двигателей илп для следящей системы радиолокационной станции сопровождения - перемещение цели.

При наличии случайных воздействий на САУ ее выходная величина будет также изменяться случайным образом, т. е. тоже будет случайной функцией времени.

Математическим аппаратом, применяемым для исследования систем, находящихся в условиях случайных воздействий, является теория вероятностей. Напомним некоторые ее положения, которые потребуются в дальнейшем.

Случа11пая величина и случайный процесс. Случайная в е л и 1 и н а - это величина, значение которой определяется неконтролируемыми нами причинами и поэтому не может быть точно предсказано. Примеры случайных величин - ошибка при стрельбе в цель, результат измерения какой-либо величины в условиях помех, результат бросания монеты или игральной кости.

Случайный процесс - это случайная величина, являющаяся функцией времени, или по-другому - это функция времепи, значение которой в каждый момент времени является случайной величино!!.

Пример случа11Н0Г0 процесса - изменение напряжения электрической сетп питания во времени. В каждый момент времени напряжение является случайной величиной. Совокупность этих величин во времени представляет собой случайный процесс. Именно случайным процессом являются случайные изменения выходной величины в системах автоматического управления.

Случайные процессы бывают стационарными и нестационарными. Стационарный случайный процесс- это случайный процесс, установившийся в статистическом смысле, когда все вероятностные характеристики его неизменны во времени. Можно сказать, что стационарных! случайный процесс является аналогом стационарного детерминированного процесса. В настоящей главе нас будут интересовать только стационарные случайные процессы.

Вместо термина случайный употребляют также термины стохастический и вероятностный.

Вероятность. Для количественной характеристики случайных величин и функций служит понятие вероятность. Введем сперва это понятие для дискретной случайной величины.

Пусть, например, такой случайной величиной х будет результат стрельбы по мишени. Обозначим через N общее количество выстрелов а Через щ - количество попаданий в мишень с выбиванием i очков (количество попаданий в кольцо на мишени, соответствующее i очкам). Тогда вероятность выбивания i очков

Р(ж,)==Ит.

(3-1)

Иными словамрг, вероятность данного значения случайной величины - это предельное значение частоты появления этого значения при увеличении до бесконечности общего количества значений этой величины.

Очевидно, что

О Р {х) 1

и сумма вероятностей всех значений случайной величины

Законы распределения случайных величин. Для полного описания случайной величиныж надо знать вероятности Р (ж.) всех ее значений, т. е. знать функцию Р (ж), которая называется законом (функцией) распределения вероятностей случайной величины.

На рис. 3-1, а приведен пример графического изображения закона распределения дискретной случайной величины.

Для непрерывных случайных величин, которые могут UiMerb бесконечное множество значений, вероятность каждого отдельного значения х- соответственно бесконечно мала, и можно говорить лишь о конечной вероятности нахождения ж в олредсленполг питер-вале значешп! между х и ж + Дж, т. е. о вероятности Р (ж ж ж -f Аж). Поэтому для описания распределения непрерывшлх случайных величин вводится понятие плотности вероятно с т и (аналогично тому; как при описании раснределепия

01 234 5 6789 6)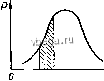

О г)

Рис. 3-1. Законы распределения случайны.х величин.

электрического тока по сечению проводника применяется понятие плотности тока). Плотность вероятности

р(Ж) = Иш

Р (xj гг xi -\- Ах)

Отсюда, в свою очередь,

Р (ж < Ж = ж -f Лж) = 5 р (ж) dx.

(3-2)

(3-3)

Графически эта величина представляет собой заштрихованную часть площади под кривой р (ж) на рис. 3-1, б.

Непрерывная случайная величина характеризуется законом (функцией) распределения плотности вероятности р(ж). Примерный вид ее показан на рис. 3-J, б. Из (3-3) следует, что площадь под кривой плотности вероятности

р (ж) dx - i.

(3-4)