I и

1ТАБЛИЦЫ

o,.*a as

3. Интегральные представления

3.1. Для л = О, 1, 2, ... имеем:

Jn J COS (z sin f-nt)dt=l.ei < - о dt (Бессель).

3.2. npHRev>-справедливы формулы (Пуассон)

J COS (z COS i) sin dt.

(z) = - . , f sin (z sin f)cos # dt - { e- h t a при -Y<Rev<y для положительных значений аргумента

ch*7 di

(Rez>0),

(Мелер, Соимн)

cosxt

3.3. Для произвольного v и правой полуплоскости {Rez>Q или ~-<arg2r<- получаем представление через контурный интеграл

+ 0 j t \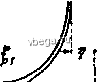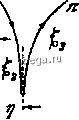

Рис. 121. Пути интегрирования в интеграле Зоммерфельда.

(Сонин)

3.4. Для произвольного v имеем (Зоммерфельд):

= J

При этом пути интегрирования выбираются следующим образом (рис. 121): для любого числа г], 0т]31, @, есть кривая, пробегаемая от -г] + /оо до 2я-T-fioo; ®j-от -Т1+/с до х\ - ioo; @,-от rj -/с до 2л; - т1+гоо. Приведенные интегральные представления Зоммерфельда справедливы в области -г)<аг§2<я; - Г).

4. Асимптотика

4.1. Асимптотические разложения Ганкеля справедливы для больших значений аргумента: lll, llv. Обозначим

(V, 0) = 1, <v, (4V-l-)(4V-3r.(4V-(2.-.)-) 3.....

и пусть Р, (г), Q, (z), 5, (z) означают следующие, формально построенные ряды *):

v -- (22)

{2z)*

(V. 1) (V. 3) (22) (2г)

формально удовлетворяющие соотношению

) Для v = 0, 1 ролучим;

, , , 0,125 , 0,0703125 0,07324219 , 0,1121521 0,2271С80 . г>Лг)=1------+--- +...,

с /о ч t . 0.375 0,1171875 , 0,10253906 0,1441956 , 0,2775764 Sj(22) = H-------t--5----5-4--5--...

*)t>. Burnett, Proc. Cambridge Philos. Soc, т. 26 (1930), стр. t45-tSI.

Тогда имеем:

Я1Н: /( * )5,(-2fe) (- <argz<2n). {г)=/е \ * *5,(2iz) (-2д<aгgг<я).

Л-)- /1 [cos (-f-I) P,()-sin (.-f-I) РЛг)

(-n<argz<n),

(-л<аг§г<я).

Эти представления надо понимать в асимптотическом смысле; если оборвать ряды 6 , Р после члена с 2 , то получим ошибку, абсолютная величина которой меньше const-1 2 и которая, следовательно, стремится к нулю при

г\- -ее. Отсюда следует, что в указанных выше областях справедливо первое приближение

Если порядок V и аргумент z = x действительны и положительны, то ошибка, получаемая при обрывании асимптотических рлдов после л-го члена, по абсолютной величине будет меньше первого отброшенного члена (и имеет для рядов Р Q, знак отброшенного члена), если только п выбрано таким, чтобы соот-

13 1

ветственно 2л>v - в Р 2л >v-g- в Q, и л>у- в 5v . Следовательно,

в практических вычислениях имеет смысл продолжать ряды только до тех пор, пока их члены убывают.

Чтобы уменьшить ошибку вычислений, получающуюся при обрывании ряда перед членом с наименьшей абсолютной величиной, можно прибавить этот член,

умноженный на /=---е (е-малая величина). Более точные выражения для множителей / даны Барнеттом*):

1) z = re f, m - \<:r<:m + l, т-целое, r==/ -f V, .~<(р f :

2) z = iy, т-1< 2 у<да-4-1, т-целое, 2y = m-ti