4. Функциональные уравнения

4.1. Справедливы следующие равенства:

. sn(-и)=-shu, сп(-ц) = спа, dn ( д) =ь dn й, sn*u + сп*а = 1, dn*a = 1 -А* sn и = к + k сп* ц = сп*цsn* а,

dn 2и + А* СП 2 4-ft*

l+dn2a l + dn2u

sn и СП и dn w i sn V СП u dn и

dnu =

l-fdn2!i

sn(a±p) = cn(tt±i ) = dn (ц±г ) =

(I-&*sn sn*0) X

.. . sn (ы, fe)

сп(ш;&)= fe)

l-A=sn- snp , dn(W, ft) - .

sn (a +i ),sn (и-г ) = sn*a -.-sn*i:>, ch (a -\-v) en (a-г ) cn*u -snV dn*a, dn (a + -w) dn (a --o) dnu -sn г cn* a.

1 - sn u sn о

en a cn g Tsn a sn g dn и dn p 1-ftsn* и sn* g

dn и dn о T fe* sn и sn g СП и cn g

4.2. Изменение функций при возрастании аргумента а на четверть- и полупериод берется из следующих таблиц, в которых для краткости написано с, d вместо sna, спи, dna:

sn(mK + nKi-f- )

cn(mK-{-nKi4- )

dn (mK 4-nK + )

4.3, Функции cn a, dn a выражаются через sna посредством соотношений сп (и, ft) = sn (ftK+fea, pj, dn ft)= ft sa(K -iK + Ш, ft).

Для перехода от одного модуля к другому имеем таблицу, где для краткости вместо sn(u, k), СП (и, к), do ( , k) пишем соответственно s, с, d:

sn (Ui, fe,)

СП ft,)

ku Uku Ши

(4+ft) (!+*)

ik k

2 V~k l+k 1 -k-l+k

Vi +

ks is

iks d

iks с

(1 + k) s l+ks< .

(!+*) f

у kAl + d)ik+d)

£ с cd

\+ks

2 1 +

+ dk + d

d. с

J

1-fes

ft)5

Vl+dVk +d

4.4. Формулы ди)ференцирования и ди)ференциальные уравнения:

iam ы , d sn ы . den и , d dn и ..

- = dnu, - = cn dn , =-snudn, -=-ftsnacna.

= (1-dn tf)(dn*u-

4.5. Формулы интегрирования:

J sn ц du = \n dn + cn

A I. Z и - ft* СП и \

= Arch 1-Arch-, = Arsh (fe Г ) = Arsh p-Arsh . СП tt arccos (dn u) = arcsin ( sn u), dn й = arcsin (sn u) = am и,

r du , cn + dnu ., С du , dnit-ffesn f j j r,/

я 0 0

* \ я;гг = arccos t- = arcsm k - , k \ - da = In , /Х--,

Jdnu \dnuj \ dnuj J спи (l-fft)cntt

. К h

Jda~ln, J = Й j e?a = --1,

0 ы 0

H К и и

.,гГпы iHJf Г drru спы fdnw- , sn ( спи sna

3dn --dn Jc-ii= =iH:7i JdH =diri;-

5. Дзета-функция Якоби za( ft) Дзета-функция Якоби (рис. 68) определяется так:

zn (и, ft) = Е{ати, ft)- ~ J dn* (в, ft) da-

Она является периодической мероморфной функцией от и (модуль ft считается постоянным) с одним периодом 2К:

2па=-zn (2К-ц)= = zn(2K + a)=-zn (-u>. 1

Нули этой функции лежат ь точках пК(пО. ± 1,. . .). .О ее представлении с помощью тэта-функций см. С, 4.3.

В. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ ВЕЙЕРШТРАССА

1. Функции Вейерщтрасса Г , ga. аи

Нормальной формой Вейерштрпсса эллиптического интеграла 1-го рода называется

Г ds

= 4{s-e,)(s-е,)(~е,).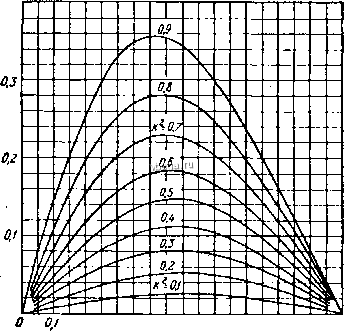

о.г 0,3 OA 0.5 0,0 07 0.8 ojf t.o

Рис. 68. zn(K-2o) как функция 2d.

Обратная функция называется эллиптической функцией Вейерштрасса и обозначается через

s=a={u] g, g,).

Она является двоякопериолической функцией комплексного аргумента и = и-\--f-(рис. 69 с огнивными периоДсАМи 2о), 2(о, которые для действительных е>е,е. Даются р..венствами

+ 1

2(0 = 2

= 21

J V -5

Величины ej, нзывчются инвпршнтами функции. Инвпризнты е нули в с . полин>ма 5 и периолы (о, со связаны paeeHCTBJMH iV u3Hj4aeT суммирование по всем отличным от нуля периодам w = 2пиа + 2п(а; /я, л = О, ± 1, ...):

g, = -4(e,e, + e,e,+e,e,)=Sf)S -1; = 4V,. = 140 J;