ИЛИ, что ТО же, в тригонометрической форме (2г=ЗШф, t-sin, Ц> = Ц>1+ ifp

f (ф, &)

Щф, я, й).

1/1-sini3rft.

(1+л зш* гз) /l -fesraif о

нлзываются неполными эллиптическими интегралами l-zo, 2-го и 3-го радо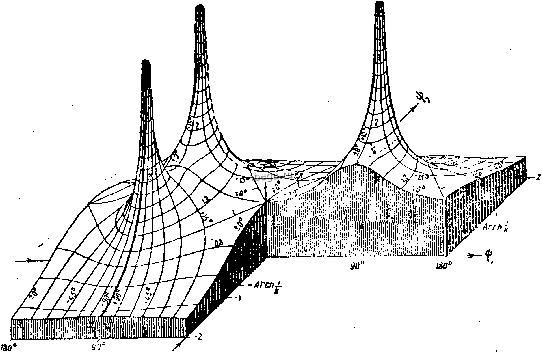

Рис. 39. Рельеф функции при 4 = 0,8. Точки ветвления ± Arch .

в нормальной форме Лежандра. Кроме того, еще вводят

Число k называется модулем интегралов, число п-параметром интеграла 3-го рода. Для краткости положим

(рис. 38, 39), причем А ( [), к)~1 в начале ij) = О пути интегрирования, и определим

k называется дополнительным модулем.

Если верхний предел интегрирования ф == -, то получаем полные эллиптические интегралы в нормальной форме. Обозначают:

Е {k) = £

2

D(k) =

-3 ACil. A)* J

~ k 2

Нормальная форма, полных интегралов, соответствующих дополнительному модулю k, обозначается так:

К(Л) = К(А). E4k) = E(k).

А. ПРИВЕДЕНИЕ ЭЛЛИПТИЧЕСКИХ ИНТЕГРАЛОВ К НОРМАЛЬНОЙ Ф0РЛ1Е

1. Общие замечания

Всякий эллиптический интеграл может быть представлен как линейная

комбинация элементарных функций и интeгpJЛOB 1-го, 2-го и 3-го родов в HopMjjibHofi форме Лежандра, Для действительных эллиптических интегралов это ирь;дставление *) можно произвести так, что модуль k в нормальных формах интс) Р.1ЛОВ н параметр л в нормлльной форме интегралов 3-го рода будут действительны и и<С<1. Верхний предел интегрирования ф может при этом

лежать в промежутке --<ф-

2, Пряведевие к нормальной форме действительных интегралов 2.1. Если преобразовать действительный эллиптический интеграл

подходящим образом выбранной подстановкой

1 +

к виду

(если афО) или x=i-г (если 0 = 0) 5 Л* {t, /±(/-Я) (*-р.)) dt.

то во многих случаях можно привести его к нормальной форме с помощью следующей вспомогательной таблицы. Она содержит в первом и. последнем

*) Формулы, необходимые в различных возможных случаях, можно найти в удобной для вычислений форме, например, в книгах: Р. F. Byrd and М. D. Friedman, Handbook of elliptic integrals юг engineers and physicists, Berlin-Gottingen-Heidelberg. 1954; F Tricomi. Funzioni b((ittiche. Bologna. 1951; J. Ной el, Recueil de formuies et de tab.es numeriques, Paris, 1901..

столбцах эллиптические интегралы, равные соответственно -F{(f>, k) или тЕ{(р, k),

причем модуль = -, а значения ф и от находятся из средних столбцов (числа а, Ь, с связаны соотношением а +- = с).

a-i-b = c\ А = , k=-

F (ф, k)

тЕ (ф, k)

+ 00

dt

J Yaf)(b + t}.

С dt

V{t + a){t - b) dt

V{a-t) (c-n dt

. Viat)(c-t)

J V{t-b){ct) b

dt 7

Vit - a) (t - cf)

+ 06

dt

V(t-a) {te)

tgT = -

sin Ф cx Д (ф, k)~ab

cos ф~ -

С03ф = ~

A (Ф, k)x sin Ф с

sin Ф = -

С05ф

A (ф, k) a А(Ф, fe) = 4-

Д(ф, k)=-

Д (Ф, k) x cos ф с

sin ф==--

6* с

c +

у {c+ty

+ 00

t+ adt tdt

л: л:

e + 1

fdt

V (t-ay{t-c)