2. интегральный Синус И интегральный косинус

2. Интегральный синус и интегральный косинус

2.1. Интегральный синус si (z) и интегральный косинус ci{z) определяются формулами

si {Z) = [Ei{iz)-EH-iz)] - J dt,

г

ci(z)= 1-1Ш{гг) + Е1<-и:)]

причем путь интегрирования долясен быть выбран так, чтобы в начале пути lim arg f = О и Imi оставалась вдоль него ограниченной.

Употребляют также следующие обозначения для этих функций:

H = si()+-- = Jrf/. Ci() = ci().

Функция si (г) является целой функцией z, а ci (г) -бесконечнозначной аналитической функцией z с единственной конечной точкой ветвления 2 = 0.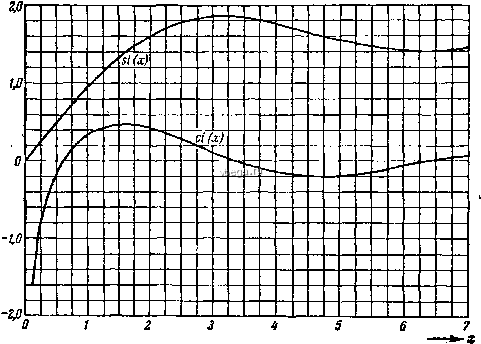

Рис. 28. Интегральный синус и интегральный косинус.

Значение функции ci (г) после т обходов вокруг точки ветвления определяется формулой

ci {ze) = ci (2) -+mni (да = О, ± I, ±2, ...)

(т. е. циклическая постоянная этой функции равна л/]. Имеют место представления

si( )=-+Х(-1) -,

-гп+1

(2п + 1)(2 --1)1

(2 ) (2г01

Отсюда ВИДНО, что

cl(.)-lйY.-]

является целой функцией z.

Функция si {X) принимает действительные значения при всех действительных значениях х, а ci(x) - при действительных л: > О (рис. 28, таблица 16). Эти действительные функции si {х) и ci {х} получаются, если для соответствующего определяющего интеграла путь интегрирования взят вдоль действительной оси, начиная с -{-оо. Имеем:

si( -д:) = -si(jc)-я, Si (-д:) = -Si (лг). Асимптотическое поведение при л: I дается формулами

~ =-( V-I+I-.. .)- (-1+§- ).

й, следовательно, в качестве первого приближения получим:

... cosx

51(л;) *-- ,

ci (х) !=и

[Обе функции имеют бесчисленное количество экстремумов (таблица 17).}

В прямоугольной системе координат (с, s) кривая c=ci(x), s = sl(jc> {х-действительный положительный параметр) представляет собой так называе-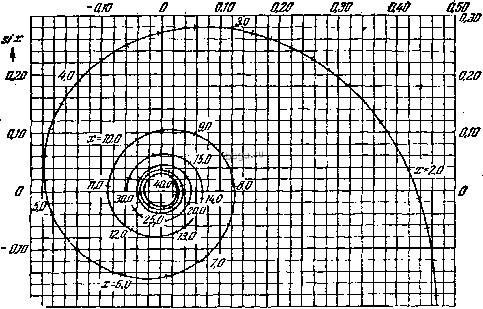

-ajf -т о шп е.2в аза

Рис. 29, sici-спираль.

~о.ао

мую sicx-cnupnAb (рис. 29). Длина дуги от начальной точки (д; = 0) до точки (ci ДГ, six) равна Injc, а кривизна я в этой точке имеет величину х-jc. Кривизна, следиВс1тельно, визрзс1ает по аксаиненциальному закину с возрастанием длины дуги.

3, Некоторые интегральные формулы

~dt: - €B\[-m{a-i-x)] . {т>0, а>0, х + а>0),

] -Т+Г -- Ei[z/ {a-[.x)3 [,ц{а + х)]л12 )

(т>0, а>0),

+ 0D

e-P*ci(qt)di = l\n[\+)

(Р>0, <7>0),

+ 00

j e- 8i(0rf--arctg- ,

+ 0 +00 .

J cos<ci<rf#= I sinsiifJ/ = -J,

+ 00 +< +06

J ci()flff= J si(Od = y , J ci(0si(0d = -In2.

2.2. Вводят функции shi (z), chi {z), называемые: интегральными гиперболическими синусом и косинусом:

2

shiU) = J=-i Si (te),

Chi (г)=c+In г+Jrf< = Ci -I.

При этом shi (г)-действительная функция для всех действительных, а chi(z) - для Действительных положительных значений z = x. [При jc>0 имеем:

.... , Ei* (je) -Ei (-je) . . , \ Ei* (;c) + Ei(-ж) и-, , \-t \ i - * shi(jc) =--i--, cTii(Jg)= {\j-5-chi (д:) + shi (x) = Li c*,

откуда получаются разложения

shi(x)=jc-- + +..-, сШИ = 1пух + + +.

функция sht(x) является нечетной:

shi(-A;) = -8Ы<л;).]