нечно, условием, чтобы отношение второй гармониг<и к первой было существенно меньшим единицы. Для сферических волн расстояние образования разрыва определяется при этом формулой

Гр = г ехр(-1/а ), (5.8)

а для цилиндрической волны -

Гр = гЛ1-1/2а ) (5.9)

§ 6. Ограниченные пучки

До сих пор рассматривались одномерные нелинейные волны. Естественно, что теория неодиомерных возмущений, хотя ее прикладное значение несомненно, становится существенно более сложной. Определенные успехи достигнуты при изучении ограниченных пучков в нелинейной среде. Уравнение во втором приближении, учитывающее нелинейные свойства среды и искажение волн одновременно с дифракционной расходимостью пучка, имеет вид [34]

дт V дх Соро дт

где Aj p=dp/dy+dp/d7 - поперечный лапласиан. Для двумерного пучка Aj p=др/ду, х - направление распространения. Это уравнение называют уравненирм Хохлова - Заболотской. Оно выведено в предположении, что поперечная компонента скорости имеет порядок \L1\ где !i =Apр(,=р7р(,<1; тем самым учитывается расходимость пучка. Изменения всех параметров волны поперек пучка происходят быстрее, чем вдоль (Уд. имеет порядок р), и при выводе этого уравнения предполагается, что

V, р = /=ч, p(ix, \i-ly, x = f-.x/Co). (6.2)

Таким образом, ограниченность пучка совместно с нелинейностью должна привести к медленным изменениям формы волны не только вдоль направления распространения, но и поперек него.

Точного решения уравнения (6.1) не получено; оно исследуется асимптотическими методами и при помощи численных методов. Приближенные решения удобно получать, вводя безразмерное число [36],- назовем его в честь Р. В. Хохлова числом Хохлова (X):

где а - ширина пучка и X - длина волны основной частоты. Число X характеризует относительный вклад нелинейных и дифракционных эффектов в искажение профиля волны, подобно тому как акустическое число Re - относительный вклад нелинейных и дис-сипативных процессов. Если X О, преобладают нелинейные эффекты и дифракцию можно не учитывать, если Х- оо, основную роль играют дифракционные эффекты. Мы не имеем возможности вдаваться здесь в подробности обсуждения нелинейной теории ограниченных пучков (см. подробное изложение вопроса в [1, 11]).

ОтметИм ЛИШЬ, ч г6 в безразмерных переменных =р/ро. =есорх/ф(, 6-сот, =г а уравнение (6.1) для плоского пучка будет иметь вид

да dQ

-Q =4-- (6.4)

4 ag.

В предельном случае X-voo, т.е. когда главными являются дифракционные эффекты, можно проанализировать уравнение (6.4), отыскивая первое приближение по малому параметру Х~. Результат показывает, что генерация гармоники в ограниченном пучке заметно отличается от того, как это происходит в плоской волне. Вначале при малых расстояниях от источника амплитуда второй гармоники на оси пучка растет линейно с расстоянием так же, как и в плоской волне. Но далее дифракция приводит к стабилизации этой амплитуды, после чего амплитуда уменьшается; имеет место (в некоторой области расстояний) аналогия с тем, как ведет себя амплитуда второй гармоники в диссипативной среде.

В случае малых чисел X -v О сильно сказывается нелинейность и в меньшей степени дифракция. Здесь нужно учесть в получающихся уравнениях члены с X не более чем в первой степени; при этом удается получить решение задачи.

Учет диссипации в уравнении (6.4) в еще большей степени усложняет его решение. В настоящее время численным методом решены задачи по применению уравнения (6.4) к анализу формы нелинейных дифрагирующих волн, поведению гармоник в пространстве и ряд других (подробнее см. [11, 37]).

Глава 4

ВЗАИМОДЕЙСТВИЯ НЕЛИНЕЙНЫХ АКУСТИЧЕСКИХ ВОЛН. ПАРАМЕТРИЧЕСКИЕ АНТЕННЫ

§ 1. Взаимодействие нелинейных волн

Вернемся снова к плоским нелинейным волнам в средах без дисперсии и рассмотрим случаи, когда в среде распространяется не одна, а несколько таких волн. Но прежде отметим следующий важный факт: нелинейное взаимодействие плоских волн конечной амплитуды в средах без дисперсии происходит эффективно лишь в том случае, когда эти волны распространяются в одном и том же направлении, т. е. коллинеарно.

Прийти к такому выводу проще всего, если рассмотреть трех-волновое взаимодействие: две волны с частотами coj и соз и волновыми числами ki=Wi/ci и k=4ijc рождают третью волну со. з= = (0з/сз, где Ci, Сз, Сз - соответствующие скорости этих трех волн. На квантовомеханическом языке можно представить плоские волны toj, k\ и (Из, кг как фононы с энергиями coi, и квазиимпульсами %ki, %k2- В случае слияния двух фононов образуется результирующий фонов о)з, Аз (при (Oi=co2 это рождение второй гармоники). Хотя понятие фонона как кванта упругой энергии возникло в применении к твердым телам (кристаллам), его можно использовать также применительно к жидкостям и газам.

На рис. 4.1 представлено такое взаимодействие, при котором должны быть выполнены условия сохранения энергии и квазиимпульса фононов (так называемые условия синхронизма для трехвол-нового взаимодействия)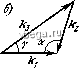

Рис. 4.1. Условия синхронизма для трехволнового взаимодействия: а) fti+

1- 2= 3-

Из приведенного геометрического построения следует, что

з V / V I / г 2 2

-COS а.

(1.1)

(1.2)