Решения уравнения Бюргерса могут быть получены при Re<l, Re l и Rel, что является существенным достоинством метода.

Хотя получение точных решений уравнения Бюргерса и оказывается возможным, в ряде случаев это представляет довольно громоздкую процедуру.

Остановимся кратко на приближенных решениях. Рассмотрим сначала случай Re<l и М<1 и воспользуемся методом последовательных приближений. Полагая v=v+v +. . ., причем v lv<\, найдем из (3.2) для первого приближения

dv b dv

где Ь/2р((=а/(о=а( - постоянная поглощения волны малой амплитуды. Если при х=0 задана гармоническая волна и и (О, t)= =U(,sin со/, то решение получается в виде (2.2.1), с которым мы уже имели дело раньше.

Уравнение для второго приближения будет иметь вид

аи b av 8 , dv ш1 , . /о с\

-3---- = -:г б~ sincoT. (3.6)

Отыскивая решение этого уравнения в виде v =v{х) чхх\2ш, получим для v{x) обыкновенное неоднородное дифференциальное уравнение

dvldx + av = (8ug(o/2c§) ехр {-2ах). (3.7)

Считая, что при х=0 имеется только волна частоты ю, а вторая гармоника отсутствует, получаем решение уравнения (3.6) в виде

v {x, т) = (еф/4аСо)(е-з -e- )sin2coT. (3.8)

Когда диссипация в среде отсутствовала (§ 1 гл. 3), то, согласно формуле (1.27), вторая гармоника возрастала пропорционально х. В рассматриваемом случае диссипативной среды на/асстояныы ста-билизации х = 1пК2/а (где нелинейный рост компенсируется диссипацией) имеется максимум для амплитуды второй гармоники; некоторое расстояние искаженная волна проходит, не меняя своей формы, после чего ее амплитуда начинает убывать, так как подкачка энергии из основной волны становится меньше, чем диссипативные потери. Заметим, что на расстояниях х, когда ах>1, о ,~ехр (-2ах), тогда как линейная волна частоты 2(о убывает быстрее. Это происходит из-за непрерывной подкачки энергии от первой гармоники во вторую.

Другое интересное решение уравнения Бюргерса, которое может быть получено без обращения к точному общему решению этого уравнения, соответствует Rel. В этом случае можно воспользоваться поэтапным рассмотрением процесса эволюции волны. Отметим сначала, что в сопровождающей системе координат формула (1.25) записывается в виде

Если воспользоваться малостью М и сохранить лишь линейные по М члены в этом выражении, то тогда во втором приближении получим

у = sin со (т + хМ/Ср).

Если в соответствии с (1.19) ввести безразмерное расстояние, равное числу длин образования разрыва а=х1 х=&ШдХС~1, то это выражение запишется в виде

у = Up sin (coT-f (Ту/Ур).

При малых X волна мало отличается от простой волны и решение совпадает с тем, которое мы записали для у выше.

Когда волна переходит в пилообразную, она стабилизируется на некотором расстоянии хх, поскольку при таких х конкуренция нелинейности и диссипации вносит примерно одинаковый вклад в эволюцию формы волны. В этом случае в уравнении Бюргерса можно пренебречь производной dvldx, и упрощенное уравнение

после двухкратного интегрирования по т дает

y = ypth(8Re(0T), (3.10)

где Ур - постоянная интегрирования. Решение (3.10) описывает стационарное возмущение, распространяющееся в нелинейной дис-сипативной среде без изменения своей формы. Это возмушение представляет собой слабую ударную волну (скачок скорости от -Ур до +Ур) с конечной шириной фронта, равной 6?:(eRe)~i.

Точное решение уравнения Бюргерса дается выражением {решение Хохлова) [20, 21]

- (от + л th f-)l, -л<(от<я. (3.11)

Безразмерная ширина фронта, как можно показать, в области стабилизации волны описывается формулой 6= (1+а) (neRe)~; ширина зависит от расстояния a=kxztA. Убывание амплитуды пилообразной волны при а>л/2, как это следует из (3.11), дается формулой

у = Ур(1+а)-1. (3.12)

Как видно, при a=kxztA=kxzvcs\ амплитуда волны не зависит от Ур. Это означает, что образование пилообразной волны (в силу ее большого поглощения) ограничивает передачу через среду большой мощности, какой бы эта мощность у источника (при х=0) ни была. После того как пила образовалась, она быстро затухает. Формула (3.11) допускает разложение в ряд Фурье {решения Фэя) [22]:

= о1Х sin( coT)sh-ii, (3.13)

п = 1

которое дает возможность при больших Re (малые 6) проследить за поведением гармоник.

Нелинейный коэффициент затухания пилообразной волны, определяемый формулой (3.12), при достаточно большой интенсивности исходной волны и не слишком малом Re может в таких маловязких жидкостях, как вода, спирты, в мегагерцевом диапазоне частот на один - два порядка превышать коэффициент затухания волн малой амплитуды а. Этот нелинейный коэффициент, согласно (3.11), имеет величину a ~aRe и может намного превышать а. Так, например, на частоте 1,5 МГц и при интенсивности 50 Вт/см-а л 10а [16]. В [1, 2] проводится подробное рассмотрение затронутых здесь вопросов, в частности приводятся решения в виде геометрических построений для определения эволюции профиля нелинейной волны, выражения для амплитуд гармоник более высоких номеров, чем второй.

а/Л=11,ЗВ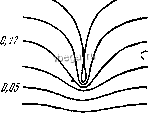

§ 4. Нелинейные плоские волны в среде с дисперсией

До сих пор рассматривались плоские нелинейные акустические волны в идеальной недиспергирующей среде и в среде с диссипацией. В акустике дисперсия не играет такой большой роли, как в оптике, в волнах на поверхности жидкости и в волнах в плазме, тем , не менее с ней часто приходится

встречаться. Так, например, в гл. 2 мы уже имели дело со слабой дисперсией среды, когда рассматривали релаксационные явления. Далее мы познакомимся с другими волновыми системами, где проявляется дисперсия,- жидкость с пузырьками воздуха, квазидисперсия при распространении звука в твердых телах, дисперсия в волноводах и т. д. Естественно, возникает вопрос, какие новые особенности появляются при распространении ,нелинейных волн в среде с дисперсией.

Наглядную картину проявления характерных черт при распространении плоской нелинейной волны в диспергирующей среде можно проследить, изучая капиллярные волны конечной амплитуды на поверхности жидкости [231. Эти волны, о которых речь шла в гл. 1, имеют скорость распространения c = Yakl(>, т. е. эти волны диспергирующие. С другой стороны, для таких волн сильно выражены нелинейные явления благодаря нелинейности уравнений движения. Например, на рис. 3.7 показана форма профиля капиллярной волны, полученная теоретически [24] при различных отношениях амплитуды волны с к ее длине к.

Рис. 3.7. Теоретическая форма профиля капиллярной волны конечной амплитуды при различных отношениях амплитуды волны к ее длине К [24].