Рассмотрим распространение плоской звуковой волны в газе или жидкости без учета диссипации. Исходными уравнениями служат: уравнение движения идеальной жидкости, которое для одномерного движения (вдоль оси х) запишется в виде

pidv/dt + vdv/dx) = - dp/dx, (1.1)

уравнение неразрывности -

р dv/dx + V др/дх = - dp/di (1.2)

и уравнение состояния -

dp/dp = cp) = f{p), (1.3)

где с(р) - скорость звука, являющаяся функцией плотности.

В гл. 2 считалось, что акустические скорости v малы и членом (©V)©, как членом второго порядка малости, можно пренебречь. Тогда из уравнений (1.1) и (1.2) легко получалось обычное волновое уравнение, описывающее процесс распространения плоской волны.

Не будем теперь пренебрегать нелинейным членом v dv/dx и попытаемся решить систему уравнений (1.1)-(1.3). Впервые такое решение было найдено Риманом в 1860 г. [12] - решение Римана.

Пользуясь (1.3), исключим давление/5 из уравнения (1.1). Получим

dv , dv dp ,1л\

dt дх р дх

Следуя Риману, введем функцию

o{p) = l(c/p)dp. (1.5)

Очевидно, что

Зст £ ф J др да с др дх р дх~ рс дх dt~ р dt

Уравнения (1.2) и (1.4) могут быть теперь записаны так:

да , да , dv dv , dv , да ,i

произведя сложение и вычитание этих уравнений, получим

(1.6)

.(a + v) + {c + v)§-ja + v)==0, ia~v) - {c~v)ja-v)0.

(1.8)

при 0==±w уравнения (1.8) сводятся к уравнениям

Ж±(±) = 0- . (1-9)

Каждое из этих двух уравнений описывает распространение возмущения (волну); одно из них распространяется в положительном направлении оси х, другое - в направлении (-а). Заметим, одна-

ко, что если в случае волнового уравнения для линейной задачи общее реитение состояло из суммы двух волн, движущихся в противоположных направлениях, то в рассматриваемом случае суммировать возмущения нельзя, поскольку возможно нелинейное взаимодействие волн, распространяющихся навстречу друг другу.

В формуле (1.9) Cj=c+v - локальная или местная скорость звука, являющаяся функцией х. Таким образом, в какой-либо точке профиля волны в области сжатия к скорости звука с прибавляется еще определенное значение колебательной скорости звука; в области разрежения будет вычитаться определенное значение v.

Учтем теперь нелинейность уравнения состояния. Согласно (I.I) имеем

Здесь везде индекс О означает равновесное сосгояине; s - энтропия; рассматриваются адиабатические процессы, s=const. Таким образом,

c = c (p/Po)(v-)/ (I.1I)

Подставляя это значение с в выражение для функции Римана (1.5), получим

Ро Ро

V-1 LVPo

(i--l) ± . (1.12)

откуда с=С(±У(7-1)2.

С учетом выражения (1.12) локальная скорость (Сд=с+и), фигурирующая в уравнении (1.9) и учитывающая вклад как нелинейности уравнения движения, так и нелинейности уравнения состояния, примет вид

C=Co±V±V{y-l)/2 = C ±£V, (1.13)

где е=(7+1)/2. Уравнение (1.9) примет вид

dv!dt-\-{c, + ev)dvldx = 0 (1.14)

(рассматриваем только волну, идущую вправо). Нелинейность уравнения движения изменяет скорость распространения возмущения на величину V (см. 1.9)), а нелинейность уравнения состояния - на величину (Y-l)v/2. Конечно, это условное разделение, поскольку уравнения реитаются совместно. Отметим, что для воздуха 7=1,40 и (7-l)/2s=:20%, тогда как для воды у=7 и (7-1)/2 300%.

Для волны, бегущей в положительном направлении х относительно неподвижной системы координат, возмущение движется со скоростью

Сл()=Со + еи = Со(1+еи/Со). (1-15)

3* 67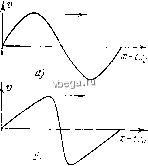

Это - скорость распространения возмущения среды в неподвижной системе координат. Отметим, что если для линейной гармонической волны u=u sinco(/-xlc), то в рассматриваемом случае, согласно (115),

у = Уо51пш(/-x/(fo-f еУ)). (1.16)

Как видно, скорость перемещения точек профиля волны различна. Точки профиля, для которых и>0, движутся со скоростями с>с (области сжатия). При о<0 имеем с<Со (области разрежения). Поэтому начальный профиль волны будет искажаться. Удобно следить за этим искажением, двигаясь вместе с волной со скоростью (сопровождающая система координат). В этой системе координат

те точки профиля, для которых у=0 ( нули волны), будут неподвижны; другие точки будут двигаться с относительной скоростью еу. На рис. 3.1 показана последовательная деформация профиля первоначально (при /=0) синусоидальной волны. BoлнaJ постепенно будет менять форму профиля, искажаться, и профиль приобретет пилообразную форму. Естественно, что такой процесс искажения будет происходить лишь до момента времени образования крутого пилообразного профиля, называемого временем образования разрыва (слабая периодическая ударная волна), поскольку захлестывание волны произойти не может; в противном случае в один и тот же момент времени каждый из трех гидродинамических параметров (у, р или р) имел бы разные значения, что не имеет смысла. По достижении пилообразной формы волна далее будет быстро затухать вследствие сильной диссипации, происходящей в тонком слое в окрестности фронта такой волны. Обращаясь к рис. 3.1, можно видеть, что заштрихованные площади при и>0 и и<:0 равны друг другу (что доказывается точно); этим пользуются для определения профиля волны после того, как она начинает захлестываться . Волна, описываемая уравнением (1.14), носит название простой волны. Обычно простой волной называют одномерную бегущую в одном направлении нелинейную волну (в этом смысле простая волна есть обобщение бегущей линейной волны на нелинейный случай), в которой каждая из переменных поля (в акустическом случае это v, р или р) может быть выражена через одну из других переменных, например р=р(и), p=p{v), c=c{v). Понятие простой волны является общим и для нелинейных волн другой физической природы. Это понятие, как, впрочем, и

Рис. 3.1. Изменение профиля плоской волны конечной амплитуды по мере ее распространения: а) t=0, б) t=ti, в) t=ty>ti, tp - время образования разрыва.