§ 5-13]

Погрешности измерений

для которого составлена таблица [5-5-5-7] 1

rflezi=Ai/a; 22=Д2/о.

Для симметричного интервала (Ai=A2= =Д) последнее выражение упрощается:

Рф{-\=.ф{г).

Если т#0, то

Нормальный закон распределения полностью характеризуется двумя параметрами-математическим ожиданием ш и дисперсией D или среднеквадр этическим отклонением о= f/D. Определить точные значения m и £) по ограниченному числу наблюдений невозможно. Однако им можно

дать приближенные оценки m и D. К указанным оценкам предъявляются требования состоятельности, несмещенности и эффективности. Оценка а параметра а называется состоятельной, если при увеличении числа наблюдений п она приближается к

параметру а. Оценка а называется несмещенной, если замена параметра а его оценкой а не приводит к систематическим ошибкам в сторону завышения или занижения,

т.е. если выполняется условие М[а]=а.

Оценка а называется эффективной, если она обладает наименьшей дисперсией по сравнению с другими.

В случае нормального закона распределения всем указанным требованиям удовлетворяют оценки

~ 1=1 m = -

I/ si

n -1

a = /5 =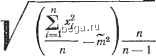

Поскольку выполнение указанных требований к оценкам зависит от вида закона распределения погрешностей, то возникает

задача проверки нормальности распределения случайных погрешностей. Эта задача решается с помощью критериев согласия. Известен ряд критериев согласия: К. Пирсона (критерий у), А. Н. Колмогорова и др. [5-5]. Однако на практике при большом числе наблюдений (п>50) предпочтение отдается критерию К. Пирсона. Сущность этого метода заключается в сравнении гистограммы экспериментальных данных с аналогичной гистограммой, построенной на основе нормального распределения.

Доверительные интервалы

Для оценки степени достоверности результата измерения пользуются понятиями доверительного интервала п доверительной вероятности.

Доверительным интервалом называется интервал /д, который с заданной вероятно стью Рд, называемой доверительной, накрывает истинное значение измеряемой величины Ои:

/д=(й--ДГ. а + Дг); Рд = Р (- y<a- й< Да),

где а - оценка величины а, полученная в р-гзультате измерения; Ai, Дг-положительные числа, определяющие длину интервала /д.

При отсутствии систематических погрешностей и известном дифференциальном законе распределения случайных погрешностей вычисление доверительной вероятности не вызывает принципиальных трудностей

= Р (- Ai < X < Дг) = J / (X) dx.

Для симметричного интервала Ai=A2=

Рд = Р(Х1<Д)= \f{x)dx.

В случае нормального закона распределения

Таким образом, если известно, что случайная погрешность подчиняется нормальному закону распределения, то, пользуясь таблицей интеграла вероятностей (функции Лапласа), можно при любом заданном доверительном интервале определить значение соответствующей доверительной вероятности, а также решить обратную задачу.

Если закон распределения случайных погрешностей неизвестен, то можно дать лишь грубую оценку точности результата измерения на основе неравенства Чебы-шева:

Р = Р(Х1<Д)> 1-.

Неравенство Чебышева устанавливает нижнюю границу доверительной вероятности. Действительная доверительная вероятность часто оказывается значительно больше. Поэтому неравенство Чебышева на практике применяется редко, только для грубых оценок.

При большом числе наблюдений (п 10-г-20) в соответствии с центральной предельной теоремой теории вероятностей

закон распределения Ли можно приближенно считать нормальным при произвольных законах распределения независимых величин Ai, причем

а а .

В этом случае доверительная вероятность

Рд = Р (Лк - Дг < Ли < Ли + Дг) 1

Для симметричного доверительного интервала

/ Д \

Рд = Р (Лк - Лк < д) л< Ф

\ Он /

Обратная задача, т. е. задача определения доверительного интервала по заданной доверительной вероятности, решается с помощью фун1щии Ч, обратной Ф. Так, половина длины симметричного доверительного интервала Д равна:

Д аиЧ(Р ).

Значения функции можно найти по таблице, составленной для функции Ф.

При малом числе наблюдений (ri<10) закон распределения среднего арифметического может отличаться от нормального закона распределения, а величина Ои значительно . отличаться от Ои. В таком случае следует применять более точные методы расчета доверительной вероятности. Однако при этом необходимо знать априорно вид закона распределения результатов отдель-Ьых независимых наблюдений.

Применительно к наиболее распростра-пенному нормальному закону распределения точный метод расчета доверительной вероятности базируется на распределении Стьюдента и доверительная вероятность вычисляется по формулам:

для несимметричного доверительного интервала

Рп = Рп

/ д, \

+ Рп

д. N

- 1,

для симметричного доверительного интервала

P =2f (- -1,

где (О-интегральная функция распределения Стьюдента. Зависимость Fn (i) от

параметров =Д/аи и п представлена таблицей [5-5-5-7].

С помощью этой же таблицы может быть решена и обратная задача - определение доверительного интервала по заданной доверительной вероятности.

Обработка прямых измерений

Обработка измерений имеет цель-дать оценку истинному значению измеряемой величины и определить степень достоверности этой оценки. Здесь рассматривается случай, при котором систематической погрешностью результата измерения можно пренебречь (оценки систематических погрешностей результата измерения рассматриваются ниже), а о законе распределения случайных погрешностей ничего не известно.

Если выполнено только одно измерение и измерительный прибор дал показание Л,

то в качестве оценки Ли истинного значения измеряемой величины Л следует принять это показание. Однако определить степень достоверности полученного результата измерения Ли невозможно, так как закон распределения случайных погрешностей неизвестен.

Если выполнено п независимых измерений одной и той же величины А{п2) а получено п результатов наблюдения at, аг,.... а .... On, то в качестве оценки истинного значения измеряемой величины берется среднеарифметическое результатов наблюдений

Ли - Ои -

где а, - результат отдельного наблюдения.

Точность полученной оценки истинного значения измеряемой величины (результата измерения) характеризуется оценкой дисперсии

~ 1=1

к (и - 1)

или оценкой среднеквадритического отклонения

Ои = Vda =

Точность метода измерения (точность одного результата наблюдения в полученной серии п результатов наблюдений) ха-

§ 5-13]

Погрешности измерений

рактеризуется соответственно величинами

Величина а позволяет дать количественную оценку степени достоверности результата измерения, т. е. найти значение доверительного интервала при заданной доверительной вероятности.

Пример [5-77]. Цифровым вольтметром произведено 10 независимых наблюдений одного и того же постоянного напряжения:

№ наблюдения 1 2 3 .4 Б

fj., мВ

2785 2841 2773 2857 2792

№ наблюдения 6 7

8 9 10

2816 2768 2822 2793 2803

Разброс результатов наблюдений связан с наличием случайных погрешностей. Систематические погрешности отсутствуют. Требуется найти;

1) оценку истинного значения измеряемого напряжения;

2) характеристики точности метода измерения d и о, а также характеристику точности Од оценки истинаого значения измеряемого напряжения;

3) приближенное значение доверительной вероятности того, что истинное значение измеряемого напряже чем на 20 мВ;

4) приближенное значение симметричного доверительного интервала, соответствующего доверительной вероятности 0,9.

Реш ени е. 1.

= 2805 мВ.

2. Для нахождения параметров d и о необходимо предварительно вычислить разности вида.

Uj-Ujj и квадраты этих разностей. Результаты вычислений сведены в таблицу:.

Далее получим: п

3 = - = 836 мВ;

п - 1

о = Vd 29 мВ; Ъи = -2- = 9 мВ.

3. А) Используя неравенство Чебышева и учитывая, что Д=20 мВ, получаем:

2 ~2

п>1-7 1--=0-8-

На этом основании результат обработки наблюдений можно представить в виде

V = 2805 ± 20 мВ

с вероятностью, большей 0,8.

Б) Второй, более точный способ вычисления доверительной вероятности дает;

Р ф( = ф(-) = 0.974;

на этом основании результат обработки наблюдений можно представить в виде

V = 2805 ± 20 мВ

с вероятностью, примерно равной 0,974. 4.

Д ои <¥ (Рд) = 9-1,645 = 15 мВ.

На этом основании результат обработки наблюдений можно представить в виде

и = 2805 ± 15 мВ с вероятностью, примерно равной 0,9.

Систематические погрешности измерений

Выделяют три источника систематических погрешностей: метод измерения, средство измерения и экспериментатор. В соответствии с этим систематические погрешности разделяют на методические, инструментальные и личные.

Методические погрешности обусловлены несовершенством метода измерения и влиянием средства измерений на объект, свойства которого измеряются. Например, потребление вольтметром тока из цепи измерения вызывает падение напряжения на внутреннем сопротивлении источника измеряемого напряжения, что приводит к методической погрешности измерения.

Инструментальные - вызываются несовершенством средств измерений, например неточностью подгонки сопротивлений резисторов, неточной градуировкой, инерционностью функциональных узлов средств измерений и т. п.

Личные - систематические погрешности, связанные с индивидуальными особенностями наблюдателя.

Обнаружение систематических погрешностей - сложная задача, особенно постоянных погрешностей, так как последние в процессе измерения ничем себя не проявляют. Поэтому и устранение систематических погрешностей производится не математической оработкой экспериментальных данных, а применением более точных методов измерений. Для этих целей в электроизмерительной технике наиболее часто пользуются методом замещения и методом компенсации погрешности по знаку.