Й;е /ftTdk в A-ft ветви; £i, ... - ЭДС Ьй; 2й; .. ветвей; Y hm - взаимная проводимость ветвей А и щ; Fftft - выходная проводимость ветви k; Jp, .... Js - токи источников в р-й..... s-fl ветвях; Нр,..., Нкз -

передаточные коэффициенты k-й и соответственно р-й, s-fl ветвей.

По определению Yi,m=Ih/Em, когда все

ЭДС, кроме JEm, равны нулю и все ветви с

источниками тока разомкнуты; Yhk=ihlEk>

когда все ЭДС, кроме Eh, равны нулю и все ветви с источниками тока разомкнуты; Hkp=IkfJp, когда все ЭДС равны нулю и разомкнуты все ветви с источниками тока, кроме ветви р.

пример (рис. 4-14,6): 1з=¥зА+¥з2Ё2. Для определения, напрнмер, Уз1=/з/Ё1 оставляем в схеме только ЭДС £1 (рнс. 4-14, д). Так как

+\(~\)/(\-=с)

Формулы преобразования соединения элементов звездой в соединение треугольником:

Y --

-23 SK

TAeW = Y + Y +Y . Г = 1/2 ; Х.1 = и т. д.

Метод подобия

Если цепь содержит один источник ЭДС или тока, то можно рассчитать все токи без составления системы Jфaвнeниfl Предполагая ток /о в одной из ветвей известным н равным, например, 1 А, определяем токи во всех ветвях и значение ЭДС или тока источника, действующего вместо заданного, чтобы получить ток 1 А. Пользуясь свойством линейности цепи, из пропорций находим токи, возникающие при действии заданной ЭДС или заданного источника тока.

Схема лииейиа, поэтому при расчетах взаимных проводимостей можно положить £1=1 В. Для вычисления взаимных проводимостей (и передаточных коэффициентов) применяют также метод подобия (см. ниже).

Преобразования схем соединения элементов треугольником и звездой

При замене соединения элементов треугольником соединением звездой сохраняются неизменными токи и напряжения для всех участков цепи, кроме преобразуемых элементов (рис. 4-15).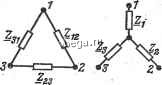

Рис. 4-15.

Формулы преобразования соединения элементов треугольником в соединение звездой:

2, 2 , 2 2,

±12 г31

?2 =

г23 1112

22

= 22

где22=2 + 2Ч-2з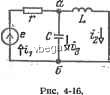

Пример (рис. 4-16). Пусть /20=! А. Тогда -)-/3 =-B=/.C-f 1; £ = г/, -Ь Ё/Ео = Р.

Действительные токи IPjii, где й=1, 2, 3.

Этот метод можно успещно применять прн вычислении взаимных проводимостей и передаточных коэффициентов.

Пример (рис. 4-14,6). Для определения J[3i= yi3 оставляем в схеме только ЭДС £i (рис. 4-14,-б) и задаем ток /з. Тогда

=->з *с L: h = 4 + h =s О - С Y

£j = г /; -h £/аб = (1 - С IL ) 4 -/С Is-

Метод подобия требует иногда предварительного преобразования соединений элементов треугольником в соединения звездой или обратно.

Если цепь содержит несколько источников ЭДС и тока, то метод подобия надо сочетать с методом наложения.

Принцип компенсации

Любой jr4acT0K с падением напряжения 2/ можно заменить источником ЭДС Ё= =2/, положительное направление которой противоположно положительному направлению тока (рис. 4-14,я и е). Такая замена не изменяет распределения токов и потенциалов в цепи. Если сопротивление Z

изменяется, то изменяются ток / и ЭДС Ё.

Теорема вариаций

В электрической цепи изменение сопротивления в какой-либо ветви q на AZg вызывает изменение тока Ip в ветви р на Д/р, причем

-qq -q

где iqo-ток в ветви q; Tpq - взаимная проводимость ветвей р к q; Fe? -входная проводимость ветви q. Значения всех величин измерены или вычислены при AZg = ==0.

Теорема взаимности

Если в цепи действует только одна ЭДС Ёа в ветви а и при этом в ветви б ток равен 1б, то при переносе этой ЭДС в ветвь б в ветви о ток 1а будет равен току /б, который раньше был в ветви б.

Линейные соотношения

При изменении сопротивления, ЭДС или тока источника в одной единственной ветви цепи все токи и напряжения попарно связаны линейными зависимостями вида у=а+Ьх, где х и у -ток любой ветви или напряжение между любыми точками, о и 6 - постоянные. Линейная зависимость при изменении тех же величин в двух ветвях имеет вид: z=a+bx+cy, где 2 -также ток или напряжение.

Пример. При изменении индуктивного сопротивления в схеме рис. 4-14, б между токами /, и /з сохраняется линейная зависимость Л- =a+bh.

Для вычисления коэффициентов с и й необходимо найти токи Ii и h при двух значениях ж, например при х =оо и х =0. При Xj = оо

(рис. 4-14, е) K=is=i=EJ(r-ixc). При =0 (короткое замыкание между точками а и в на рис. 4-14,6) Л=(В,+ё2)/г; h-EH-iXf)-Составляем два уравнения;

K/i - Ус ) = + ь Ё/(г ~ ixc ):

(E + EjIra-i-bElixc, из которых определяются коэффициенты с и Ь.

Передаточная функция

В цепи с одним источником энергии, в частности, предназначенной для передачи и преобразования сигналов (информации), отношение величины, которая принята выходной, к заданной (входной, известной) определяется передаточной (схемной, системной) функцией Н цепи. Например, в комплексной форме

где индекс k относится к выходной величине, а индекс т - к входной. В частности, взаимные проводимости, передаточные коэффициенты и т.п. можно рассматривать как передаточные функции.

Пример. Для цепи рис. 4-16 передаточная функция между током h и током источника Ii

el v

1Пе>С

jaL -Ь 1 (оС

При изменении частоты тока, ЭДС или напряжения источника

Я = Я(/(а) = Я((й)е*<*),

где Я(й))-амплитудно-частотная характеристика; ч1)((й)-фазо-частотная характеристика; HQa) - амплитудно-фазовая характеристика (на комплексной плоскости - годограф). Если ЯС/ш) - безразмерная величина, то ]пЯ(/ш)=1пЯ(й))--/ч1)(й))-логарифмическая амплитудно-фазовая характеристика.

Об обозначении напряжений иа схемах

Для уточнения записи законов Кирхгофа и обобщенного закона Ома всегда необходимо указывать на схемах положительные направления токов и ЭДС. Записывая напряжения, следует указывать индексами, какое напряжение записано:

lJa6 = Ча - фб ИЛИ Оба = фб - фс

(рис. 4-17);

Ua6==~U6a = E + Zi (рис. 4-17,а);

Ua6=-lJBa--E + Z[ (рис.-4-17,6).

Стрелки для ЭДС ставятся иногда не внутри источника, а рядом с ним.

йаб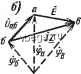

Рис. 4-17.

Сигнальные графы

Любую систему линейных уравнений, описывающую режим линейной электрической цепи, можно наглядно изобразить в виде сигнального графа, который состоит из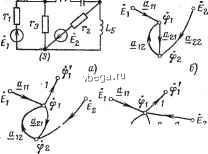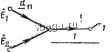

£22 f ; iZZttrZ

Рис. 4-18.

узлов и соединяющих узлы направленных ветвей. Узлы отображают зависимые переменные величины цепи (токи ветвей и напряжения на участках) и независимые (ЭДС и токи источников), ветви - коэффициенты при переменных в системе уравнений.

Для построения сигнального графа по системе уравнений каждая зависимая пе-

ременная представляется как функция всех других переменных (независимых и зависимых). Например, для схемы рис. 4-18, а по методу узловых потенциалов при фз=О получаются уравнения

у =.-1---L ,

гз /((oL-l/oC) у у = \

/(C0L4-l/(uQ)

/-2 / ((uZ,4- l/(uQ) /(OLg

1 2

Из уравнения (1) определяется потенциал ф1 первого узла, а из уравнения (2) потенциал фг второго:

Ф1 = £11 1+ 12Ф2;

(3) (4)

&1=-Г21/Г22; ?22=-Ж2;

здесь следует иметь в виду, что Оуфоц.

Уравнения (1), (2) или (3), (4) содержат две зависимые (фь qi) и две независимые (£(, £2) переменные. Поэтому граф имеет четыре узла (рис. 4-18,6). Ветвь соединяет соответствующие узлы, если коэффициент, который определяет передачу ветви, ОгкЧО, и направлена к узлу г.

в общем случае граф имеет узлы- истоки, к которым присоединены только

выходящие ветви (£i и на рис. 4-18,6), промежуточные узлы с входящими и выходящими ветвями (ф1 и q)2 на рис. 4-18,6) и узлы -стоки, к которым присоединены только входящие ветви. В сток можно преобразовать любой промежуточный узел, добавляя ветвь с единичной передачей. Например, у графа рис. 4-18, е, эквивалентного графу рис. 4-18,6, есть сток Ф1=Ф1.

Для определения искомой величины, например потенциала фь надо исключить из системы уравнений остальные зависимые переменные [из уравнений (1), (2) или (3), (4) потенциал фг]. Исключению зависимой переменной соответствует основное преобразование графа - исключение промежуточного узла.

Правила исключения промежуточного узла в простейших графах показаны на рис. 4-19, о-е, где цифрами обозначены